Relato: Geometria Plana: Construindo o Tangram no GeoGebra

Nome: Elena Maria Piva Marin
E-mail: elenapiva@gmail.com
Instituição: Colégio Estadual Dario Vellozo
Município: Toledo - Pr
Conteúdo: Geometria Plana - Construindo o Tangram no GeoGebra
Série: 8ª (9º ano)

---

Proposta de atividade

• Construção de um Tangram de sete peças no software GeoGebra.

Conteúdos de geometria plana que podem ser explorados por meio dessa atividade

• Ponto médio
• Semelhança de triângulos
• Retas paralelas, perpendiculares e concorrentes
• Área e perímetro de triângulos e quadriláteros
• Relações entre medidas dos comprimentos dos diferentes segmentos de reta e dos perímetros e das áreas das figuras que constituem o Tangram.

Passo a passo para construção do Tangram no Geogebra

1. No menu Exibir, clique em Malha para que a malha fique visível na tela do GeoGebra. Clique em eixo para ocultá-lo.
2. Utilize a ferramenta Polígono e crie um Polígono Regular. Clique na área de trabalho e crie o ponto A. Em seguida crie o ponto B 8 unidades à direita do ponto A na malha. A partir da medida do segmento AB, construa o quadrado ABCD.
3. Escolha a ferramenta Segmento definido por dois pontos para construir a diagonal DB.
4. Utilizando a ferramenta Ponto médio, encontre o ponto médio dos segmentos: DB, CD e CB
5. Com a ferramenta Segmento definido por dois pontos, trace uma reta paralela a DB, criando o segmento FG. Encontre o ponto médio de FG.
6. Trace uma reta perpendicular à diagonal DB, criando os segmentos AG e GH.
7. Crie os segmentos DG e GA e encontre o ponto médio desses dois segmentos.
8. Trace o segmento EJ e HK.
9. No menu exibir, clique em malha para ocultá-la.

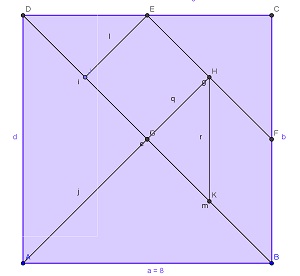
Tangram construído no GeoGebra


Fonte da imagem: a autora


Atividades após a construção do Tangran

1. Complete com números: o Tangram é formado por ___ peças, sendo, ___ triângulos: ___ grandes, __ médio e ___ pequenos, ___ quadrado e ___ paralelogramo.
2. Identifique os segmentos paralelos, perpendiculares e concorrentes no Tangram.
3. Na ferramenta ângulo, escolha cm, clique em cada segmento para dar as medidas e calcule:
   • a área e o perímetro de cada figura
   • a razão de semelhança entre os triângulos grande, médio e pequeno
   • a razão dos perímetros dos triângulos.
   • a razão de semelhança entre o quadrado maior e o menor.
   • que fração o triângulo maior corresponde do quadrado formado pelas 7 peças.

Referências

PANADÉS RUBIÓ, Angel e FREITAS, Luciana Maria Tenuta de. Matemática e suas tecnologias. São Paulo: IBEP, 2005
PARANÁ. Secretaria de Estado da Educação. Diretrizes Curriculares da Educação Básica. Matemática.  Curitiba, Seed, 2006.
IEZZI,GELSON; DOLCE, Osvaldo e MACHADO, Antonio Machado. Matemática e Realidade. 6 ed. São Paulo: Atual, 2009