Relato: Ângulos

Nome: Monica Thumer Metzler Bueno
E-mail: monicametzlerb@gmail.com
Instituição: Colégio Estadual Santa Catarina
Município: Coronel Domingos Soares - Pr
Conteúdo: Ângulos
Série: 8ª / 9º ano

---

Este material foi elaborado como requisito de avaliação final da oficina de GeoGebra, sob orientação da docente, assessora pedagógica Rosani Terezinha Hulse, da equipe da Coordenação Regional de Tecnologia Educacional do Núcleo Regional de Educação, de Pato Branco.

Justificativa

Os ângulos estão presentes no futebol, por exemplo, um chute "no ângulo" significa que o artilheiro conseguiu visualizar a trajetória da bola antes do chute, fazendo o gol. Um construtor de molduras vai precisar cortar cada lado do quadro em 45 graus para que as 4 hastes se encaixem sem folga. Um engenheiro que precisa medir grandes terrenos usa um equipamento especial para medição de ângulos, chamado teodolito. Com o resultado - e com o uso de funções da trigonometria, como seno, cosseno e tangente - ele consegue estimar grandes distâncias. Um militar operando um lançador de projéteis terá que calcular o alcance da bomba com base no ângulo do disparo - ou seja, o ângulo que a arma faz com o solo. Um mecânico fará o alinhamento das rodas de um carro com base no ângulo que elas devem fazer com o eixo do automóvel.

Povos da Antiguidade fizeram várias medições importantes com o uso de ângulos - o grego Erastótenes, por exemplo, conseguiu estimar o diâmetro da Terra apenas medindo diferenças de ângulo de sombras em diferentes pontos. O relógio de sol é outra aplicação do estudo de ângulos de sombras. Portanto, o estudo dos ângulos se faz necessário e para tal estudo faremos uso do software o Geogebra onde estudaremos os ângulos através de um feixe de retas parelelas.

Objetivo

Construir um feixe de paralelas cortadas por uma transversal para demonstrar as propriedades do teorema, utilizando o software Geogebra.

Encaminhamento Metodológico e recursos didáticos

Primeiramente, na sala de aula, apresentar as definições do teorema. Em seguida no laboratório de informática, utilizar o software Geogebra, para construir um feixe de paralelas e calcular as medidas dos ângulos e dos segmentos formados pelas retas, com base nos procedimentos apresentados em anexo. Finalizar as atividades com a discussão e análise dos resultados encontrados.

Avaliação

Participação e envolvimento dos alunos no desenvolvimento das atividades propostas.

Referências

PARANÁ, Secretaria de Estado da Educação. Diretrizes Curriculares a Educação Básica – Matemática.
Curitiba: Seed, 2007.

ANEXOS

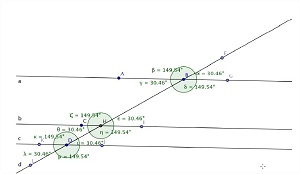
Atividade 1: Ângulos formados por um feixe de paralelas cortada por uma transversal.

a) Retire os eixos coordenados e a malha;
b) Construa uma reta definida por dois pontos A e B;
c) Defina outro ponto C e trasse uma reta paralela a reta anterior e que passe por C;
d) Construa uma reta que passe por A e C e seja transversal as retas paralelas;
e) Renomeie essa transversal como t;
f) Determine pontos sobre as retas para que possa calcular os ângulos formados;
g) Calcule as medidas dos ângulos e compare.


  Acesse imagem ampliada


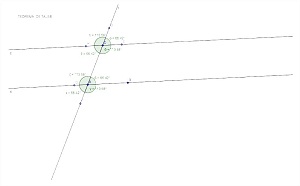
Atividade 2: Ângulos formados por um feixe de paralelas cortada por uma transversal.

a) Retire os eixos coordenados e a malha;
b) Construa uma reta definida por dois pontos A e B;
c) Defina outro ponto C e trasse uma reta paralela a reta anterior e que passe por C;
d) Construa uma reta que passe por A e C e seja transversal as retas paralelas;
f) Renomeie essa transversal como t;
g) Defina outro ponto D e trasse uma reta paralela a reta anterior e que passe por D;
g) Determine pontos sobre as retas para que possa calcular os ângulos formados;
h) Calcule as medidas dos ângulos e compare.



Acesse imagem ampliada