Relato: Geometria Plana e Geometria Analítica
Nome: Joarez Barcelos de MouraE-mail: jobar@proserv.com.br jobar@proserv.com.br e joarez@seed.pr.gov.br
Instituição: Colégio Estadual Dom Carlos
Município: Palmas - Pr
Conteúdo: Geometria Plana e Geometria Analítica
Série: 3ª do Ensino Médio
Este material foi elaborado como requisito de avaliação final da oficina de GeoGebra, sob orientação da docente, assessora pedagógica Rosani Terezinha Hulse, da equipe da Coordenação Regional de Tecnologia Educacional do Núcleo Regional de Educação, de Pato Branco.
Justificativa
Faz-se necessário utilizar a tecnologia em prol da humanidade, sem que isso venha a causar distúrbios que traumatizam os seres humanos. Podemos assim, afirmar que para uma boa aprendizagem a seleção de conteúdos matemáticos seja coerente com a realidade contemporânea, onde o educando precisa galgar os degraus do conhecimento de maneira progressiva sem transtornos por métodos diretos. É preciso munir nossos alunos com ferramentas as quais eles usarão em suas vidas acadêmicas e, somente assim eles se apossarão dos conhecimentos matemáticos desenvolvidos ao longo dos tempos na história da humanidade.
Sendo assim, o software Geogebra é uma das ferramentas disponíveis aos alunos e que possibilita uma maneira diferente de aprender.
Objetivos
- Demonstrar a construção de polígonos regulares inscritos entre si e suas relações métricas.
- Determinar o cálculo da distância entre dois pontos numa reta.
- Determinar as coordenadas do ponto médio de um segmento de reta em função dos vértices do polígono.
- Incentivar os alunos para a construção de polígonos regulares com a utilização do software Geogebra para verificar o centro do pentágono e os cálculos de ângulos, áreas, perímetro e segmentos de retas.
Encaminhamento Metodológico e Recursos Didáticos
Este tipo de atividade esta voltada aos alunos do ensino médio após já terem estudado os conceitos de geometria plana e geometria analítica, independente da série, de acordo com o PTD de seus professores.
Esta atividade pode ser desenvolvida no Laboratório de Informática e também em sala de aula. No laboratório, com o uso do Software Geogebra e em sala de aula, com uso de papel milimetrado, réguas, esquadros e compasso. É uma atividade prazerosa em que pode ser desenvolvida individualmente ou em duplas. É importante ressaltar que o professor precisa trabalhar a teoria como pré-requisito para a execução da tarefa. Aí, então, já no laboratório explica o passo a passo da tarefa para que todos consigam realizá-la.
Avaliação
Observar o interesse e a participação em atividades desenvolvidas em grupo para busca de soluções adequadas na realização dos exercícios propostos.
Anexos
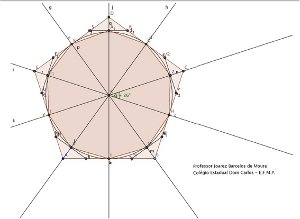
A construção do decágono regular inscrito num pentágono regular.
Seja ABCDE um pentágono regular de lado l; a bissecção de seus cinco ângulos centrais nos fornecerá o decágono regular, que é determinado pela ligação de cada vértice do pentágono com o respectivo centro por meio de uma reta a qual secciona o lado oposto, em seu ponto médio. Os outros vértices do decágono regular serão obtidos dos respectivos pontos médios, através das simetrias axiais.
Atividades de construção
1) Construa um pentágono regular de lado 5 cm.
2) Determine o ponto médio de cada lado do pentágono regular.
3) Trace diagonais interligando cada vértice ao ponto médio do lado oposto.
4) Determine a intersecção, de no mínimo, duas dessas diagonais para determinar o centro desse pentágono regular.
5) Construa uma circunferência inscrita neste pentágono. O que você observa?
6) Determine o ponto médio de cada segmento de reta de extremos ponto médio do item 2 até o vértice subsequente.
7) Trace retas ligando-as do ponto médio ao ponto médio do lado oposto de cada vértice.
8) Marque o ponto de intersecção (ponto de simetria axial) entre uma dessas retas com a diagonal do vértice do pentágono.
9) Trace os segmentos de reta interligando cada ponto de simetria axial ao ponto médio do pentágono regular.
10) Com a Ferramenta Polígono, interligue cada vértice do decágono regular. Pronto. Esta criado o decágono regular inscrito num pentágono regular.
11) Determine a área do pentágono regular.
12) Determine a área do decágono regular inscrito no pentágono regular.
13) Determine a diferença entre a área do pentágono regular com a área do decágono regular inscrito.
14) Determine o perímetro de cada polígono.
15) Determine o número de diagonais de cada polígono.
16) Determine a medida de cada ângulo interno do decágono regular. O que você observa?
Referências
EVES, Howard. Introdução à história da Matemática / Howard Eves; tradução: Hygino H. Domingues. Campinas, SP: Editora da Unicamp, 2004.
FERREIRA, Aurélio Buarque de Holanda. Novo Aurélio Século XXI: O dicionário da Língua Portuguesa. 3. ed. Totalmente revista e ampliada. Rio de Janeiro: Nova Fronteira, 1999.
GIOVANNI, José Ruy. Matemática Fundamental: uma nova abordagem: Ensino Médio: volume único. José Ruy Giovanni, José Roberto Bonjorno, José Ruy Giovanni Jr. – São Paulo: FTD, 2002.
PARANÁ Secretaria de Estado da Educação. Diretrizes Curriculares da Educação Básica: Matemática. Curitiba, Seed, 2008.

