Relato: Função do primeiro grau no GeoGebra

Nome: Sandro Ferreira Delgado
E-mail: sandrodelgado9@hotmail.com
Instituição: Colégio Estadual Padre Ponciano
Município: Palmas - Pr
Conteúdo: Função do primeiro grau
Série: 8ª / 9º ano

---

Este material foi elaborado como requisito de avaliação final da oficina de GeoGebra, sob orientação da docente, assessora pedagógica Rosani Terezinha Hulse, de Pato Branco.

Justificativa

O estudo da função do primeiro grau é muito importante no estudo de variações de grandezas em diferentes situações e também, na análise de gráficos usados no nosso dia a dia.
A função do primeiro grau, além da Matemática, é usada em outras áreas do conhecimento, como na física, na química, na biologia e em outras ciências.
Conseguimos interpretar melhor os dados de uma função, por meio de construções no software Geogebra.

Objetivo

Construir gráficos de situações problemas que envolvem função do primeiro grau, utilizando o software Geogebra, mostrando as raízes da função e verificando se a função é crescente ou decrescente.

Encaminhamento Metodológico e recursos didáticos

Primeiramente, na sala de aula, rever os conceitos de função do primeiro grau e os conceitos de raízes ou zeros da função. Em seguida no laboratório de informática utilizando o software Geogebra, construir alguns gráficos de função do primeiro grau para estudar os zeros da função e ver na pratica quando a função é crescente ou decrescente, os procedimentos para isso será apresentado em anexo.
Finalizar as atividades com a discussão e análise dos resultados encontrados.

Avaliação

Participação e envolvimento dos alunos no desenvolvimento das atividades propostas.

Referências

BONJORNO, José Roberto; BONJORNO, Regina Azanha; BONJORNO, Ayrton Olivares. Matemática: Fazendo a diferença. 1º Ed.- São Paulo: FTD, 2006.
GIOVANNI jr, José Ruy; GIOVANI JR, Jose Ruy; CASTRUCCI, Benedito. A conquista da matemática. 9º ano. São Paulo: FTD, 2009.

ANEXO

Atividade 1: Construir um gráfico de uma função.
Função polinomial do primeiro grau é definida em ƒ: R?R por y= ax + b, com a e b reais e a? 0.
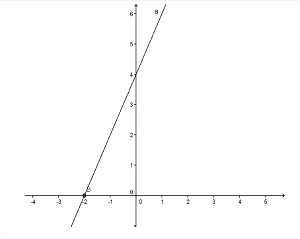
a) Usando a entrada algébrica digite a função y= 2x + 4.
b) Fazer a intersecção ente a função e o eixo x.
Obs.: Explicar que este ponto da intersecção entre a função e o gráfico é raiz ou zero da função, pois neste ponto a função tem valor igual a zeros.


Acesse imagem ampliada

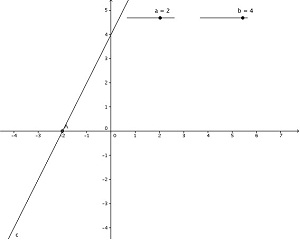
Atividade 2:Construir um gráfico de uma função usando seletor.
a) Construa dois seletores a e b.
b) Usando a entrada algébrica digite a função y= a*x+b.
c) Fazer a intersecção ente a função e o eixo x.
d) Movimente o seletor para ver o que acontece com a reta da função.
Obs: Explicar quando a função é crescente e quando ela é decrescente.




Acesse imagem ampliada


Atividade 3: Usando exemplo do cotidiano.
– Uma pessoa vai escolher um plano de saúde entre duas opções A e B.
– O plano A cobra R$ 10,00 de inscrição e R$ 30,00 por consulta num certo período.
– O plano B cobra R$ 18,00 de inscrição e R$ 40,00 por consulta num mesmo período.
O gasto total de cada plano é dado em função do numero x de consulta, desta forma qual dos planos é mais econômico.



Acesse imagem ampliada


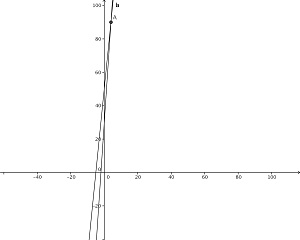
Obs.: Pelo gráfico podemos visualizar que com quatro consultas os planos A e B tem preços iguais, a partir de cinco consultas o plano A passa a ser mais econômico que B.