Relato: Geometria Analítica
Nome: Daniela Bierhals BrennerE-mail: fabrenner@hotmail.com
Instituição: Colégio Estadual Santo Agostinho
Município: Palotina - PR
Conteúdo: Geometria Analítica
Série: 3ª
Este material foi elaborado como requisito de avaliação final da oficina GeoGebra, sob orientação dos docentes, assessores pedagógicos Sandro Albarello e Maximiliano Tomazini, da equipe da Coordenação Regional de Tecnologia Educacional do Núcleo Regional de Educação, de Toledo.
Relato
Ao trabalhar com a Geometria, sabemos da importância da visualização dos desenhos, para haver uma melhor compreensão dos conteúdos. Nem sempre dispomos de tempo para fazer usando lápis e papel vários gráficos, polígonos, retas, circunferências, ângulos com medidas corretas. Quando conheci o software Geogebra, percebi que tudo isso é possível de ser realizado com menos tempo e com grande eficácia. É possível mudar medidas, deslocar figuras, ampliar, reduzir, comparar gráficos diferentes com facilidade.
Inicialmente foi trabalhado em sala de aula com a equação geral da reta, inclinação e coeficiente angular de uma reta, cálculo do coeficiente angular, posição relativa de duas retas: retas paralelas e retas perpendiculares.
Depois disso, usamos o software Geogebra para visualizar o que já tínhamos estudado. Trabalhamos com quatro situações diferentes.
1 - Fornecendo duas equações de retas paralelas 2x + y = 5 e –4x - 2y = -1, mostramos que a inclinação das duas retas é a mesma, ou seja, seu coeficiente angular é igual. (Conforme passo a passo nº 1).
2 - Fornecendo duas equações de retas perpendiculares 27x –9y –1 = 0 e 2x +6y –3 =0, mostramos que o coeficiente angular de uma reta é o inverso e o simétrico da outra reta. (Conforme passo a passo nº 2).
3 - Fornecendo dois pontos definimos uma reta. Por um terceiro ponto definimos uma reta paralela à anterior. Traçando uma reta que cortasse as duas retas definidas, mostramos que o ângulo formado pelas retas paralelas com a transversal é o mesmo.(Conforme passo a passo nº 3).
4 -Fornecendo dois pontos definimos uma reta.Construímos uma reta perpendicular à primeira e mostramos que o ângulo formado pelas duas retas perpendiculares é de 90º. (Conforme passo a passo nº 4).
Objetivos
- Identificar a inclinação de uma reta e seu coeficiente angular.
- Calcular o coeficiente angular de uma reta, conhecendo a equação geral da reta.
- Determinar as posições relativas entre duas retas no plano comparando os respectivos coeficientes angulares.
Passo a passo 1
1 - Abra o software Geogebra.
2 - Clique no menu Arquivo e selecione Gravar como. Salve o arquivo com o seguinte nome: Retas Paralelas.
3 - Selecione a ferramenta Inserir texto e clique sobre a área de trabalho, onde deseja que apareça o texto. Digite: RETAS PARALELAS. Clique em aplicar.
4 - Clique com o botão direito do mouse sobre o título da atividade e selecione Propriedades. Selecione a guia Cor e escolha um tom de vermelho. Escolha a guia Texto e mude o tamanho da fonte (letra) para 18 e clique em N para que o texto fique em negrito. Depois clique em fechar.
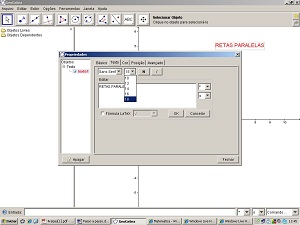
Acesse imagem ampliada5 - No menu Exibir clique em Eixo para que este fique oculto.
6 - No menu Exibir clique em Malhas para que esta fique oculta. Caso as malhas não estejam aparecendo, não precisa realizar esse passo.
7 - Vamos usar o campo de entrada que deve estar visível na parte inferior da área de trabalho. Caso não esteja aparecendo esta janela clique no menu Exibir e selecione Campo de Entrada.
8 - No campo de entrada, digite a reta: 2x + y = 5. Dê um Enter. Esse comando criará a reta da equação dada.
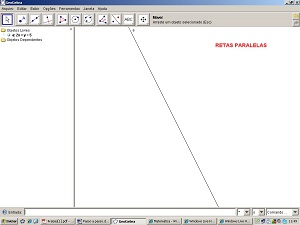
Acesse imagem ampliada9 - No campo de entrada, digite a reta: -4x – 2y = -1. Dê um Enter.
10 - Selecione a ferramenta Inclinação. Aproxime o cursor de cada reta e só clique quando cada uma estiver destacada e aparecer a mensagem que a identifica.
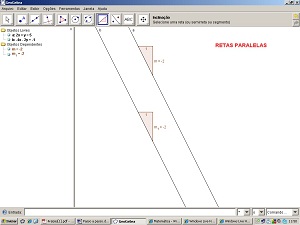
Acesse imagem ampliadaPasso a passo 2
1 - Abra o software Geogebra
2 - Clique no menu Arquivo e selecione Gravar como. Salve o arquivo com o seguinte nome: Retas Perpendiculares.
3 - Selecione a ferramenta Inserir texto e clique sobre a área de trabalho, onde deseja que apareça o texto. Digite: RETAS PERPENDICULARES. Clique em aplicar.
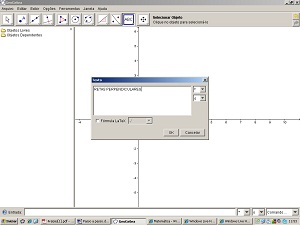
Acesse imagem ampliada4 - Clique com o botão direito do mouse sobre o título da atividade e selecione Propriedades. Selecione a guia Cor e escolha um tom de azul. Escolha a guia Texto e mude o tamanho da fonte (letra) para 18 e clique em N para que o texto fique em negrito. Depois clique em fechar.
5 - No menu Exibir clique em Eixo para que este fique oculto.
6 - No menu Exibir clique em Malhas para que esta fique oculta. Caso as malhas não estejam aparecendo, não precisa realizar esse passo.
7 - Vamos usar o campo de entrada que deve estar visível na parte inferior da área de trabalho. Caso não esteja aparecendo esta janela clique no menu Exibir e selecione Campo de Entrada.
8 - No campo de entrada, digite a reta: 27x - 9y –1 = 0. Dê um Enter. Esse comando criará a reta da equação dada.
9 - No campo de entrada, digite a reta: 2x + 6y –3 =0. Dê um Enter.
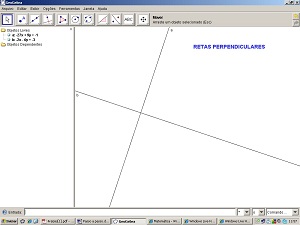
Acesse imagem ampliada10 - Selecione a ferramenta Inclinação. Aproxime o cursor da reta e só clique quando cada uma estiver destacada e aparecer a mensagem que a identifica.
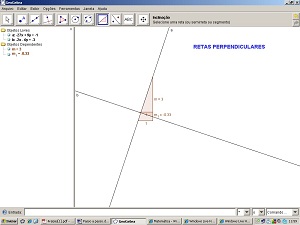
Acesse imagem ampliadaPasso a passo 3
1 - Abra o software Geogebra
2 - Clique no menu Arquivo e selecione Gravar como. Salve o arquivo com o seguinte nome: Retas Paralelas.
3 - Selecione a ferramenta Inserir texto e clique sobre a área de trabalho, onde deseja que apareça o texto. Digite: RETAS PARALELAS. Clique em aplicar.
4 - Clique com o botão direito do mouse sobre o título da atividade e selecione Propriedades. Selecione a guia Cor e escolha um tom de verde. Escolha a guia Texto e mude o tamanho da fonte (letra) para 16 e clique em N para que o texto fique em negrito. Depois clique em fechar.
5 - No menu Exibir clique em Eixo para que este fique oculto.
Acesse imagem ampliada6 - No menu Exibir clique em Malhas para que esta fique oculta. Caso as malhas não estejam aparecendo, não precisa realizar esse passo.
7 - Digite na caixa de entrada os seguintes pontos A=(3,2), B=(-3,-1) e C=( 10,2). Para isso digite um ponto de cada vez.
8 - Selecione a ferramenta Reta definida por 2 pontos. Clique sobre o ponto A e depois sobre o ponto B. Você construirá a reta a.
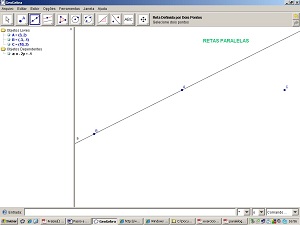
Acesse imagem ampliada 9 - Selecione a ferramenta Reta Paralela. Clique sobre o ponto C e depois sobre a reta a. Você construirá a reta b.
10 - No campo de entrada digite a reta y=1.
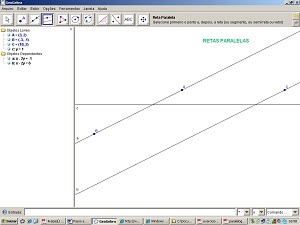
Acesse imagem ampliada 11 - Selecione a ferramenta Intersecção de dois objetos. Clique no cruzamento das retas a e c e b e c após perceber que ambas estão destacadas. Surgirão os pontos D e E.
12 - Selecione a ferramenta Novo Ponto e clique sobre a reta c em 2 lugares, definindo os pontos F e G.
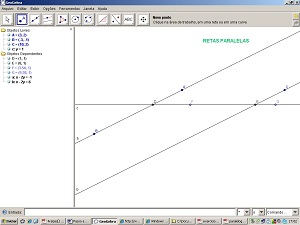
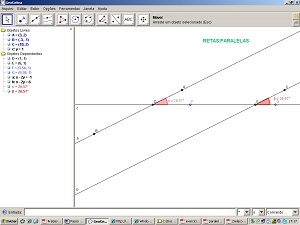
Acesse imagem ampliada 13 - Selecione a ferramenta Ângulo. Clique nos pontos FDA e GEC.
14 - Clique com o botão direito do mouse sobre um ângulo e selecione Propriedades. Selecione a guia Cor e escolha um tom de vermelho e na guia Estilo escolha o tamanho 50 e preenchimento 50. Faça o mesmo para o outro ângulo.
Acesse imagem ampliada Passo a passo 4
1 - Abra o software Geogebra
2 - Clique no menu Arquivo e selecione Gravar como. Salve o arquivo com o seguinte nome: Retas Paralelas.
3 - Selecione a ferramenta Inserir texto e clique sobre a área de trabalho, onde deseja que apareça o texto. Digite: RETAS PERPENDICULARES. Clique em aplicar.
4 - Clique com o botão direito do mouse sobre o título da atividade e selecione Propriedades. Selecione a guia Cor e escolha um tom de roxo. Escolha a guia Texto e mude o tamanho da fonte (letra) para 18 e clique em N para que o texto fique em negrito. Depois clique em fechar.
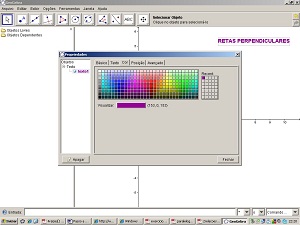
Acesse imagem ampliada 5 - No menu Exibir clique em Eixo para que este fique oculto.
6 - No menu Exibir clique em Malhas para que esta fique oculta. Caso as malhas não estejam aparecendo, não precisa realizar esse passo.
7 - Selecione a ferramenta Novo ponto. Clique em 2 lugares aleatórios. Serão definidos os pontos A e B.
8 - Selecione a ferramenta Reta definida por 2 pontos. Clique sobre o ponto A e depois sobre o ponto B. Você construirá a reta a.
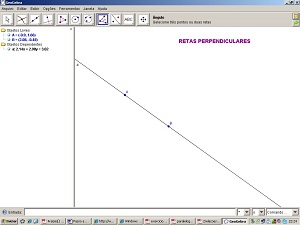
Acesse imagem ampliada 9 - Selecione a ferramenta Reta perpendicular. Clique na reta a e num ponto fora dela. Estará definida a reta b, perpendicular à reta a.
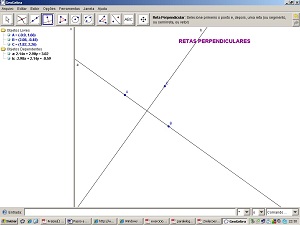
Acesse imagem ampliada10 - Selecione a ferramenta Intersecção de dois objetos. Clique no cruzamento das retas a e b após perceber que ambas estão destacadas. Surgirá o ponto D.
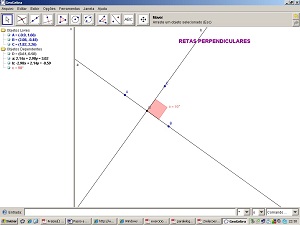
11 - Selecione a ferramenta Ângulo. Clique nos pontos BDC.
12 - Clique com o botão direito do mouse sobre um ângulo e selecione Propriedades. Selecione a guia Cor e escolha um tom de vermelho e na guia Estilo escolha o tamanho 70 e preenchimento 50.
Acesse imagem ampliada Referências
GOULART, Márcio Cintra. Matemática no Ensino Médio. 3ª série. São Paulo: editora Scipione, 2008.
GIOVANNI, José Ruy e BONJORNO, José Roberto. Matemática Completa. 3ª série. São Paulo: FTD, 2005.
