Relato: Número Pi

Autora: Debora da Silva Nascimento
Instituição: Colégio Estadual Alberto Santos Dumont
Município: Campo Mourão - Pr
Conteudo: Numero Pi
Série: 7ª (8º ano)

---

Este material foi elaborado como requisito de avaliação final da oficina Geogebra, sob orientação da docente, assessora pedagógica Giselli Mocelin Martins, da equipe da Coordenação Regional de Tecnologia na Educação do Núcleo Regional de Educação, de Campo Mourão.

Relato

Neste encaminhamento propõe-se um modo de demonstrar ao aluno que a razão entre o comprimento e o diâmetro de uma circunferência resulta sempre na constante irracional pi (?).

Objetivos

• Mostrar a obtenção do número irracional ? (pi) utilizando a Geometria.
• Relacionar o comprimento e o diâmetro de uma circunferência.
• Compreender, identificar e reconhecer o número ? como um número irracional especial.

Desenvolvimento metodológico

Após explorar o conceito de número irracional, o professor poderá levar os alunos a relacionar o comprimento e o diâmetro de uma circunferência com o número irracional ?, bem como realizar cálculos que envolvem esse número irracional.

Para determinar o valor ?, os alunos poderão ser organizados em grupos para realizar uma atividade, por meio da manipulação de material concreto, onde precisarão de barbante, régua e vários objetos cilíndricos com tamanhos diferentes como moedas, latas vazias de óleo, de alimento etc. Enquanto os alunos manipulam esses materiais cilíndricos, o professor poderá enfatizar o significado de circunferência e de diâmetro.

Cada aluno poderá medir o perímetro e o diâmetro dos objetos trazidos, registrarem as medidas encontradas e a razão entre elas, observar que os resultados são muito parecidos, isto é, algo próximo a 3,14... Depois o professor orientara os alunos de que farão uma aula prática no laboratório de informática utilizando o programa Geogebra e que através deste programa eles poderão construir, identificar e observar que independente do comprimento da circunferência o valor do número irracional ? será constante.

O professor orientará todo o processo de desenvolvimento da aula, explicará o passo a passo de toda a construção no Geogebra e acompanhará individualmente os alunos que apresentarem alguma dificuldade.

Recursos

Os recursos utilizados serão: livro didático, quadro-negro, giz, apagador, barbante, régua, objetos cilíndricos, laboratório de informática e software Geogebra.

Avaliação

A avaliação será um processo que envolve a:

• Utilização dos recursos e metodologias observando constantemente sua adequação.
• Observação e realização das atividades em sala de aula e laboratório de informática.
• Participação do aluno nas diversas atividades individuais e em grupo.

Referências

BIGODE, Antonio J. L. Matemática hoje e feita assim. 2 ed. São Paulo : FTD, 2000.
DANTE,L.R. Tudo e matemática. 2.ed. São Paulo: Ática, 2008.
GIOVANNI, C.; GIOVANNI, Jr.. A conquista da matemática. 8o ano – ed.Renovada São Paulo: FTD, 2009.
IEZZI, G.; DOLCE, O; MACHADO, A. Matemática e realidade. 5. ed. São Paulo: Atual,2005.
PARANA. Secretaria de Estado da Educação. Diretrizes Curriculares da Educação Básica. Curitiba: Seed, 2008.

Passo a passo da atividade

1. Abra o software (programa) GeoGebra.
2. Clique com o botão direito do mouse e aparecerá Janela de visualização, clique em Eixos para que este fique oculto, caso esteja visível.
3. Clique com o botão direito do mouse e aparecerá Janela de visualização, clique em Malhas para que este fique oculto, caso esteja visível.
4. Clique no B6 e selecione circulo definido pelo centro e um dos seus pontos, dê um clique na área de trabalho, mova o mouse e dê outro clique para fixar o raio do círculo.
5. Clique no B3 e selecione reta definida por dois pontos. Clique no ponto A depois no ponto B.
6. Para encontrar a intersecção da reta com a circunferência, clique no B2 e selecione intersecção de dois objetos. Clique sobre a reta e dê outro clique sobre a linha da circunferência. Observe que no ponto B aparecerá o ponto C1, clique com o botão direito do mouse sobre ele e desmarque a opção exibir objeto.
7. Clique com o botão direito sobre a reta e desmarque exibir objeto.
8. Clique no B3 e selecione segmento definido por dois pontos e clique sobre os pontos C e D. Clique com o botão direito sobre o segmento, aparece uma janela propriedades, na opção nome escreva d, em seguida na opção exibir rotulo selecione nome e valor e clique em fechar.
9. No B7, selecione distancia ou comprimento e clique na circunferência.
10. Clique com o botão direito do mouse sobre o texto circunferência, clique em editar, selecione a palavra circunferência antes do sinal de igual e digite C, clique aplicar. Na janela de álgebra clique com o botão direito sobre circunferência, selecione renomear e digite C.
11. No campo de entrada, digite C/d e dê enter. Qual o valor da razão C/d?
12. Clique no B1 selecione mover e movimente o ponto A ou B. O que acontece com o valor do comprimento da circunferência? E do diâmetro?
13. Observe o valor do b na janela de algebra. Ele sofre alguma alteração? Como é conhecida esta constante?

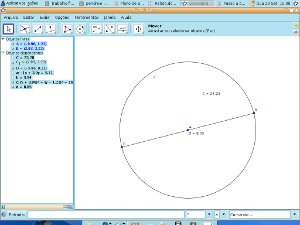
Veja abaixo a imagem da tela do Geogebra com a construção