Relato: Triângulos
Autora: Luciana Aparecida dos SantosInstituição: Colégio Estadual Alberto Santos Dumont
Município: Campo Mourão
Disciplina: Matemática
Conteúdo: Triângulos
Série: 7ª Série (8º Ano)
Este material foi elaborado como requisito de avaliação final da oficina Geogebra, sob orientação da docente, assessora pedagógica, Giselli Mocelin Martins, da equipe da Coordenação Regional de Tecnologia na Educação do Núcleo Regional de Educação, de Campo Mourão.
Justificativa
O estudo da geometria leva o aluno a desenvolver o raciocínio matemático através do exercício de abstração dos conceitos geométricos e, também, através dos exercícios de indução e dedução de resultados.
O desenho geométrico é de fundamental importância para reforçar o aprendizado de resultados fundamentais da geometria plana, elementar e também para construir a representação dos objetos geométricos que são trabalhados nessa ciência.
A fim de permitir a construção e manipulação de construções geométricas, observando suas propriedades e relações, será utilizado o software de geometria dinâmica GeoGebra, disponível nos laboratórios das escolas.
Objetivos
- Identificar e representar triângulos.
- Reconhecer e representar os elementos do triângulo: vértices, lados, ângulos internos.
- Classificar os triângulos quanto às medidas de seus lados e quanto às medidas de seus ângulos internos.
- Identificar o ponto de encontro desses elementos.
Desenvolvimento metodológico
Explorar o pré-conhecimento que os alunos já possuem de ângulos e por meio disso classificar triângulos como figuras que possuem três ângulos. Identificar triângulos na sala de aula e em ambiente externo, notando a existência de diferentes triângulos, manipular materiais como canudos, tiras de papelão e outros similares formando figuras. Após esse trabalho, informar aos alunos que eles terão uma aula prática no laboratório de informática, utilizando o programa GeoGebra e que através desse software eles poderão construir, observar, identificar e reconhecer todos os elementos de um triângulo, construindo assim seu próprio material de estudo e pesquisa, podendo ainda modificar, criar novas hipóteses e alterar medidas.
O educador orientará todo o processo de desenvolvimento da aula, explicará o passo a passo de toda construção no GeoGebra e acompanhará individualmente os estudantes que apresentarem alguma dificuldade.
Recursos
Sala de aula, canudos, tiras de papelão, computador com software GeoGebra.
Referências
GIOVANNI, Júnior, José Ruy. A conquista da Matemática. 8º ano- ed. Renov. São Paulo: FTD, 2009.
PARANÁ. Secretaria de Estado da Educação. Diretrizes Curriculares da Educação Básica. Matemática Curitiba: Seed, 2008.
Passo a passo das atividades no GeoGebra
Atividade A
1) Abra o software (programa) GeoGebra.
2)Clique no meu Arquivo e selecione Gravar como. Digite o nome do arquivo: Estudando Triângulos. Salve o arquivo numa pasta.
3)Selecione a ferramenta Inserir texto e clique sobre a área de trabalho, onde deseja que o texto apareça. Digite: Estudante: Nome. Digite enter no teclado. Digite a data. Clique em aplicar.
4)Selecione a ferramenta Inserir texto e clique sobre a área de trabalho, onde deseja que o título da atividade, apareça. Digite: Estudando Triângulos. E clique em aplicar.
5)Selecione a ferramenta Mover. Clique sobre o texto segure o mouse pressionado e arraste-o para posicioná-lo melhor, caso não tenha ficado no lugar desejado.
6) No menu Exibir clique em Eixos para que ocultá-los, caso estejam visíveis.
7) Selecione a ferramenta Polígonos(5), clique na área de trabalho, mova o mouse 6 espaços para a direita de mais um clique, mova 4 espaços para baixo de mais um clique,mova mais 6 espaços para esquerda e clique novamente, para fechar a figura clique no ponto inicial formando assim um retângulo. Com a mesma ferramenta, clique nos pontos A, B, C e A. Que figura se formou?
8) Clique com o botão direito do mouse sobre a parte inferior do retângulo na janela que se abre desmarque a opção Exibir Objeto para que fique somente um triângulo.
9) Selecione a ferramenta Distância ou comprimento (7) e clique em cada um dos lados do triângulo. O que apareceu na tela? O que estes valores significam?
10)Com a ferramenta Ângulo, clique dentro do triângulo para marcar seus ângulos internos. Esse e um Triângulo Retângulo.
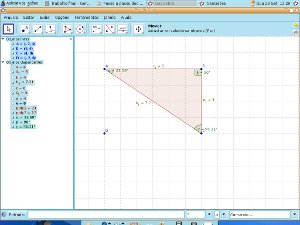
a) Quais características você observa nesse triângulo?
b) Como você justificaria o seu nome?
11) Com a ferramenta Mover(1), arraste o ponto C até que dois de seus ângulos fiquem iguais.
a) O que aconteceu com a medida seus lados?
b) Ele continua sendo um triângulo retângulo?
c) Qual é a medida dos seus ângulos internos?
12) Com a ferramenta Mover(1), arraste um dos pontos até que as medidas de seus lados fiquem iguais.
a) Como ficaram as medidas dos seus ângulos?
b) Qual é a soma dos seus ângulos internos?
c) O que tem em comum com a soma dos ângulos internos dos dois triângulos?
Atividade B
a) Crie dois pontos A e B. Construa o segmento a (segmento AB).
b) Crie um ponto C (de preferência abaixo do segmento AB). Construa uma reta b, perpendicular ao segmento AB, passando pelo ponto C.
c) Marque o ponto D (interseção da reta com o segmento). E marque o ponto E (ponto médio entre C e D). Construa a reta c (reta que passa por E e é paralela a a).
d) Construa o segmento d (segmento AC) e e (segmento BC). Marque os pontos F (ponto de interseção de c e d) e o ponto G (ponto de interseção de c e e). Marque os ângulos internos do triângulo.
e) Construa o triângulo DBG e os triângulos ADF e FGC.
f) Retire os rótulos desnecessários (Editar – propriedades).
g) Crie um seletor ? com variação de 0° a 180°.
h) Depois selecione a ferramenta girar em torno de um ponto por um ângulo (8).
Clique no triângulo DBG em seguida no ponto G. Abrirá uma janela, em ângulo escreve ? e selecione a opção sentido horário. Mover o seletor até 180°, clicar no triângulo DBG e ocultar este triângulo.
Repita o processo para o triângulo ADF, porém selecione a opção sentido anti-horário.
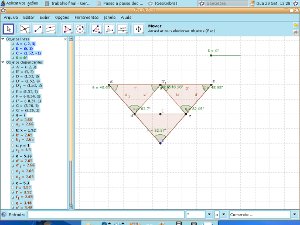
i) Que conclusões se podem tirar quando giramos o seletor de 0° para 180°? O que você observa com relação aos ângulos que coincidem no vértice C? Como é denominado esse ângulo? O que podemos concluir com relação à soma dos ângulos internos de um triângulo? Essa conclusão é valida para todos os tipos de triângulos?
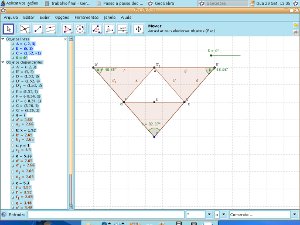
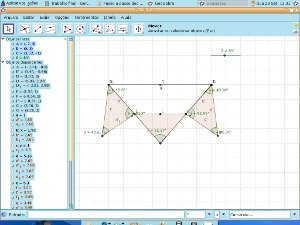
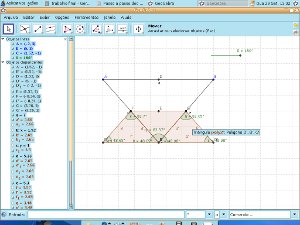
Telas da construção, observando a rotação dos triângulos
i) Que conclusões podem-se tirar quando giramos o seletor de 0° para 180°? O que você observa com relação aos ângulos que coincidem no vértice C? Como é denominado este ângulo? O que podemos concluir com relação à soma dos ângulos internos de um triângulo? Essa conclusão é valida para todos os tipos de triângulos?
Telas da construção, observando a rotação dos triângulos