Relato: Pontos notáveis de um triângulo - Baricentro

Autor: Amilton Roberto Agnolin
Instituição: Colégio Estadual Professor João Farias da Costa
Município: Campo Mourão
Conteúdo: Pontos Notáveis de um Triângulo - Baricentro
Série: 7ª, 8º ano

---

Este material foi elaborado como requisito de avaliação final da oficina Geogebra, sob orientação da docente, assessora pedagógica Giselli Mocelin Martins, da equipe da Coordenação Regional de Tecnologia na Educação do Núcleo Regional de Educação, de Campo Mourão.

Justificativa

Através do programa Geogebra podemos explorar a geometria com maior agilidade e melhor visualização, proporcionando aos nossos educandos, conteúdos do currículo de maneira que a construção do conhecimento seja de forma prazerosa e efetiva.

Pretende-se desenvolver o conteúdo de geometria, sobre Pontos Notáveis de um Triângulo – Baricentro, utilizando os recursos dos computadores com o aplicativo Geogebra, disponível nos computadores do Paraná Digital ou até na rede de internet.

Objetivos

• Construir triângulos a partir de três pontos distintos.
• Conhecer e localizar ponto médio de uma reta.
• Conhecer e construir medianas em um triângulo.
• Localizar o ponto do baricentro de um triângulo.
  

Desenvolvimento metodológico

O professor fará em sala de aula uma retomada de conteúdo sobre: ângulos, ponto, ponto médio, reta, segmento de reta, reta perpendicular, reta paralela, altura de um triângulo. O professor apresenta um problema para que os alunos possam refletir sobre o assunto a ser desenvolvido.

O professor relacionará o baricentro com o ponto de equilíbrio de um triângulo. Para verificar essa propriedade, os alunos em grupos construirão um triângulo qualquer em uma cartolina e localizarão o baricentro, em seguida irão colar um fio no ponto encontrado para verificar se houve o equilíbrio. Esse equilíbrio será verificado suspendendo o triângulo pelo fio (o triângulo ficará livre no ar, sustentado pelo fio) e os alunos deverão observar se ele permanece na posição horizontal, caso isso ocorra, o ponto encontrado é exatamente o baricentro, caso isso não ocorra (se o triângulo ficar inclinado), significa que o ponto encontrado não é o baricentro do triângulo. Em seguida, o professor explicará sobre o baricentro, que é o centro de gravidade do triângulo, e a importância da precisão das medidas no momento de se encontrar esse ponto.

Nos computadores do Paraná Digital, os alunos poderão verificar a construção do baricentro, por meio da tecnologia, associando a agilidade e podendo fazer experiências com tamanhos e formatos diferentes, com construções rápidas e práticas.

Com o Geogebra do laboratório PRD, o professor proporá a atividade de construção do baricentro de um triângulo, aliando a teoria da sala de aula à prática com os recursos da informática.

Recursos

• Lápis, borracha, régua, transferidor, compasso, esquadro, cartolina, cola, barbante, tesoura, caderno, computador com o aplicativo Geogebra.

Referências

PARANÁ. Secretaria de Estado da Educação. Diretrizes Curriculares da Educação básica. Matemática.  Curitiba: Seed, 2008.

PROJETO Aribabá. Matemática 7ª série. 1. ed. São Paulo: Moderna, 2006.

Passo a passo para construção do triângulo

1. Abra o software (programa Geogebra).
2. Clique no menu Arquivo e selecione Gravar como: digite o nome do arquivo:
3. Selecione a ferramenta inserir texto e clique sobre a área de trabalho, onde deseja que o texto seja apareça. Digite seu nome. Clique enter. Digite a data. Clique em aplicar.
4. Selecione a ferramenta inserir texto e clique sobre a área de trabalho, onde deseja que o título da atividade apareça. Digite: Pontos Notáveis de um Triângulo – O Baricentro e clique em aplicar.
5. Selecione a ferramenta mover B1, clique sobre o texto, segure o mouse pressionado e arraste para melhor posicionar, caso não tenha ficado no lugar desejado.
6. No menu exibir, clique em eixos, para que este fique oculto, caso esteja visível.
7. No menu exibir, clique em malhas, para que esta fique oculta, caso esteja visível.
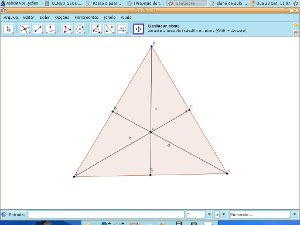
8. Selecione a ferramenta novo ponto B2, clique em três pontos quaisquer na janela geométrica, criando os pontos A, B e C.
9. Selecione a ferramenta segmento de reta definida por dois pontos B3 e clique sobre os pontos AB, AC e BC.
10. Selecione a ferramenta ponto médio ou centro B2, clique nos pontos AB, AC e BC, criando os pontos médios: D, E e F. Selecione a ferramenta mover B1 e mova os pontos médios, o que acontece? Mova os vértices do triângulo, o que acontece com os pontos médios?
11. Selecione a ferramenta segmento definido por dois pontos B3, clique ligando o vértice A ao ponto médio E. Clique ligando o vértice B ao ponto médio D. Clique ligando o vértice C ao ponto médio F. Como são denominados esses segmentos?
12. Selecione a ferramenta intersecção de dois objetos B2. Clique sobre o segmento AE e depois sobre o segmento BD, determinando o ponto G. Como é denominado este ponto? Mova um dos vértices do triângulo, o segmento CF também passa pelo ponto G?
13. Selecione a ferramenta mover B1 E arraste os vértices do triângulo para visualizar as diferentes posições do baricentro da figura. O ponto G é sempre interno ao triângulo? Mova o ponto G, isso é possível? Por quê?

Veja a seguir a tela final da construção do Baricentro no Geogebra.