Relato: Bissetriz e ângulos opostos pelo vértice
Autora: Sandra Maria PitaInstituição: Colégio Estadual Professor João Farias da Costa – EFM
Município: Campo Mourão
Conteúdo: Bissetriz e Ângulos Opostos pelo Vértice
Série: 6º ano
Este material foi elaborado como requisito de avaliação final da oficina Geogebra, sob orientação da docente, assessora pedagógica Giselli Mocelin Martins, da equipe da Coordenação Regional de Tecnologia na Educação do Núcleo Regional de Educação, de Campo Mourão.
Justificativa
O trabalho com Geometria implica o desenvolvimento de um tipo especial de pensamento, que permite compreender, descrever e representar, de forma organizada, o mundo em que se vive. Sendo preciso compreender as propriedades dos objetos, suas posições relativas, representações no plano, perspectivas, etc.Percebemos que o trabalho com o espaço e as figuras geométricas vem sendo negligenciado no ensino fundamental e pouco explorado no ensino médio e estamos diante de um desafio que apresenta uma proposta de trabalho com Matemática que vise à aprendizagem significativa. Para tanto devemos dispor de diferentes meios para esse fim. O Geogebra se apresenta como uma proposta diferente da oferecida em sala de aula através do quadro, régua, compasso e transferidor oportunizando ao aluno, além de desenvolver o conteúdo o contato com diferentes mídias tecnológicas.
Objetivos
- Reconhecer e construir a bissetriz de um ângulo.
- Verificar que ângulos opostos pelo vértice são sempre congruentes.
Desenvolvimento metodológico
Após o desenvolvimento do conteúdo específico: Bissetriz e ângulos opostos pelo vértice em sala de aula, abordando os aspectos fundamentais do conteúdo como o conceito de bissetriz e o que são ângulos opostos pelo vértice, os alunos orientados pelo professor resolveram atividades que envolvam a construção de uma bissetriz e a medida de ângulos opostos pelo vértice com o uso de régua, compasso e transferidor. Realizadas as atividades os alunos serão levados ao laboratório de informática para que possam utilizar o programa Geogebra, a fim de realizar atividades para obter a bissetriz de um ângulo e também constatar que ângulos opostos pelo vértice são congruentes, isto é, apresentam a mesma medida. Os alunos serão orientados durante as atividades pelo professor que acompanhará individualmente os alunos que demonstrarem dificuldades.Recursos
Em sala de aula serão usados, além dos recursos humanos (professor e alunos) recursos materiais como: livro didático, caderno, lápis, borracha, transferidor, régua e compasso. No laboratório de informática computadores e o software Geogebra.Avaliação
Os alunos serão observados no decorrer e desenvolvimento das atividades, com relação ao interesse e participação durante o uso do programa Geogebra.Referências
PROJETO Aribabá. Matemática. Obra coletiva. 1. ed. São Paulo: Moderna, 2006.PARANÁ. Secretaria de Estado da Educação. Diretrizes Curriculares da Educação Básica. Matemátiva. Curitiba: Seed, 2008.
Passo a passo da atividade
1) Abra o software (programa) Geogebra.
2)Clique no meu Arquivo e selecione Gravar como. Digite o nome do arquivo (File name): Ângulos Opostos pelo Vértice e Bissetriz. Salve o arquivo na pasta do aluno.
3) Selecione a ferramenta Inserir texto (3I) e clique sobre a área de trabalho, onde deseja que o título, onde deseja que o texto apareça. Digite: Alunos: Nome completo 1 e nome completo aluno 2. Dê um Enter no teclado. Digite a Data. Clique em aplicar.
4) Selecione a ferramenta Inserir texto (3I) clique na área de trabalho, onde deseja que o título da atividade, apareça. Digite: 1º Atividade – Bissetriz
5) Selecione a ferramenta Mover (1A). Clique sobre o texto, segure o mouse pressionando e arraste-o para posicioná-lo melhor, caso não tenha ficado no lugar desejado.
Atividade 1 – Bissetriz
Construa um ângulo utilizando a ferramenta reta definida por dois pontos 1C, clique na área de trabalho e aparecerá o ponto A, mova o mouse e de outro clique para fixar a reta e aparecerá o ponto B, temos uma reta passando pelos pontos A e B.
Vamos obter um terceiro ponto, o ponto C clicando sobre o ponto A em um lugar qualquer da área de trabalho. Observe que aparecerá uma segunda reta passando pelos pontos A e C.
Identifique o ângulo BÂC e vamos medí-lo usando a ferramenta 1G (ângulo) clicando sobre os pontos C, A e B nessa ordem. Aparecerá a medida do ângulo.
Usando a ferramenta 4D (bissetriz) clique sobre os pontos B, A e C nessa ordem e aparecerá uma nova reta. Qual o nome dessa reta? O que ela faz com relação ao ângulo?
Clique sobre a ferramenta 1B e insira um novo ponto sobre a bissetriz e meça o ângulo BÂD, usando a ferramenta 1G, clicando nos pontos D, A e B nessa ordem. Qual a medida desse ângulo? Obtenha a medida do ângulo CÂD, usando a ferramenta 1G, clicando nos pontos C, A e D. Qual a medida desse ângulo? Qual a relação entre o ângulo BÂC e os ângulos BÂD e CÂD?
Usando a ferramenta 1A (mover) clique e arraste o ponto B. O que acontece com relação à medida dos ângulos quando você aumenta ou diminui a abertura entre as retas?
Clique na caixa de entrada e verifique se a soma dos ângulos BÂD e CÂD é igual à medida do ângulo BÂC.
Atividade 2 - Ângulos Opostos pelo Vértice
Clique sobre a bissetriz com o botão direito do mouse e na janela exibir objeto para ocultar a bissetriz.
Vamos inserir o ponto E na reta que contém o ponto C usando a ferramenta 1B
(novo ponto) clicando acima do ponto A.
Insira o ponto F na reta que contém o ponto B usando a ferramenta 1B, clicando no abaixo do ponto A.
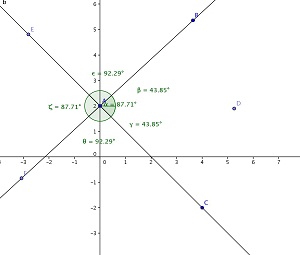
Quais são os pares de ângulos opostos pelo vértice?
Vamos medir os pares de ângulos opostos pelo vértice usando a ferramenta 1G clicando sobre os pontos que formam os respectivos ângulos:
- Ângulo: BÂC- clique sobre os pontos C, A e B nessa ordem;
- Ângulo: EÂF- Clique sobre os pontos E, A e F nessa ordem;
- Ângulo: BÂE- clique sobre os pontos B, A e E nessa ordem;
- Ângulo: CÂF- clique sobre os pontos F, A e C nessa ordem.
Quantos graus mede a soma desses quatro ângulos?
Usando a ferramenta 1A (mover) movimente o ponto C e observe o que acontece com a medida dos ângulos.
Tela do Geogebra com a construção