Relato: Distância entre dois pontos no plano, ponto médio de um segmento, retas paralelas e equação

Autora: Angela Maria Alves Angeli
Instituição: Colégio Estadual Campina da Lagoa – EFMPN
Município: Campo Mourão - PR
Conteúdo: Distância entre dois pontos no plano, ponto médio de um segmento, retas paralelas e equação da reta.
Série: 3ª Ensino Médio

---

Este material foi elaborado como requisito de avaliação final da oficina Geogebra, sob orientação da docente, assessora pedagógica Giselli Mocelin Martins, da equipe da Coordenação Regional de Tecnologia na Educação do Núcleo Regional de Educação, de Campo Mourão.

Justificativa

A forma como a Matemática vem sendo ensinada na sala de aula não tem acompanhado a evolução social e tecnológica e nem correspondido as exigências atuais. É notável a insatisfação dos alunos que não entendem e não compreendem a relevância do conhecimento matemático.
O uso do computador no ensino da Matemática poderá proporcionar avanços no processo ensino-aprendizagem, contribuindo e desafiando professores e alunos a torná-lo um aliado importante na construção do conhecimento.
O software GeoGebra tem a vantagem didática de apresentar, ao mesmo tempo, duas representações diferentes de um mesmo objeto que interagem entre si: sua representação geométrica e sua representação algébrica.
É mais uma ferramenta que pode oferecer a oportunidade de dinamizar e consolidar o trabalho pedagógico em matemática.
A geometria analítica estuda as figuras geométricas associadas a um sistema de coordenadas. Sendo assim, as figuras podem ser representadas por meio de pares ordenados, equações ou inequações. Ela trata os problemas geométricos utilizando os recursos da álgebra. Isso se dá pela substituição de pontos por números e pares ordenados de números e de retas e curvas por equações.
Por meio da Geometria Analítica, problemas como cálculo de distância entre pontos, coordenadas de ponto que divide um segmento conforme uma razão dada, determinação de pontos de intersecção de curvas, discussão de curvas, entre outros no campo da astronomia e da mecânica, podem ser solucionados.
O estudo de geometria facilita a aprendizagem da matemática, pois proporciona a visualização do pensamento e a percepção do significado de conceitos e símbolos.
A aprendizagem torna-se mais consistente quando o aluno compreende e se apropria do objeto de estudo.
Objetivos

• Identificar e utilizar os conceitos sobre plano cartesiano, distância entre dois pontos, ponto médio de um segmento para a resolução da questão proposta;
• Calcular distâncias entre pontos no plano;
• Obter o ponto médio de um segmento a partir de seus extremos;
• Reconhecer retas paralelas e suas equações;
• Determinar intersecção de retas;
• Reconhecer a conexão entre álgebra e geometria;
• Destacar a importância do uso das tecnologias no ensino-aprendizagem da matemática;
• Favorecer a experimentação, tornando a aula interessante e motivadora e a aprendizagem da Matemática significativa e agradável.

Desenvolvimento metodológico

Após introdução sobre o conteúdo de Geometria Analítica, conceitos básicos e prévios terem sido explorados e discutidos, dedução de fórmulas, resolução de exercícios e problemas, construções e demonstrações no plano cartesiano, feitos com régua, no quadro e no caderno em sala de aula, será utilizado o laboratório de informática da escola para realizar a atividade proposta.
Já no laboratório, será feita uma orientação sobre o programa Geogebra, como acessá-lo, como utilizar seus recursos e como ele pode facilitar as representações, as construções, a visualização e, consequentemente a aprendizagem.
Após todas as instruções, a professora apresenta a questão a ser desenvolvida com a ajuda do software, acompanha o passo a passo, individualmente, conforme a necessidade dos alunos.

Recursos

Os recursos utilizados ainda na sala de aula são: livro didático, quadro negro, giz, apagador, régua, esquadro, caderno, lápis, borracha, entre outros. No laboratório de informática: computador, software Geogebra, pen-drive, papel com instruções sobre como a atividade deve ser resolvida (passo a passo).

Avaliação

A avaliação será feita através da observação sobre:

• o interesse por diferentes maneiras de solucionar a questão;
• a percepção das características e regularidades das formas geométricas;
• atitudes positivas em relação ao conteúdo estudado;
• o ato de saber comunicar o pensamento e se envolver na construção do conhecimento matemático;
• a capacidade de criar novos procedimentos corretos e simples para resolver a questão.

Referências

DANTE, L. R. Matemática: ensino médio: livro do professor. volume único. São Paulo: Ática, 2008.
PARANÁ. Secretaria de Estado da Educação. Diretrizes Curriculares da Educação Básica. Matemática. Curitiba: Seed, 2008.
RUBIÓ, Angel Panadés; FREITAS, Luciana Maria Tenuta de. Matemática e suas tecnologias: ensino médio: livro do professor. São Paulo: IBEP, 2005.
SILVA, Cláudio Xavier da; BARRETO FILHO, Benigno. Matemática aula por aula. São Paulo: FTD, 2005.

Passo a passo da atividade

Sendo A(3, -5), B(5, -3) e C(-1, 3) os vértices de um paralelogramo ABCD. Determine o ponto de intersecção das diagonais e o quarto vértice.

1. Abra o software (programa) Geogebra.
2. No campo de entrada digite (3,-5) enter, (5,-3) enter e (-1,3) enter.
3. Construa os segmentos AB e BC usando a ferramenta segmento definido por dois pontos (B3). Clique no ponto A e no ponto B, novamente no ponto B e no ponto C.
4. Construa uma reta paralela ao segmento BC. Pegue a ferramenta reta paralela (B4), clique no ponto A em seguida no segmento BC. Observe na janela de álgebra, o que apareceu?
5. Construa uma reta paralela ao segmento AB. Pegue a ferramenta reta paralela (B4), clique no ponto C em seguida no segmento AB. Observe a equação da reta, qual é seu coeficiente linear?
6. Usando a ferramenta intersecção de dois objetos (B2) clique na intersecção das duas retas construídas. O que aconteceu? O que este ponto representa? Quais são as coordenadas deste ponto?
7. Construa a diagonal do paralelogramo com a ferramenta segmento definido por dois pontos (B2). Clique no ponto A em seguida no ponto C.
8. Sobre esta diagonal determine o ponto médio com a ferramenta ponto médio ou centro (B2) clique no ponto A em seguida no ponto C. Quais são as coordenadas deste ponto?
9. Construa a outra diagonal do paralelogramo com a ferramenta segmento definido por dois pontos (B2). Clique no ponto B em seguida no ponto D.
10. Determine o ponto de intersecção das diagonais com a ferramenta intersecção de dois objetos (B2), clicando na intersecção das duas diagonais. Que ponto apareceu? O que este ponto tem em comum com o ponto médio? Porquê isso acontece?
11. Clique sobre as duas retas paralelas (uma de cada vez) com o botão direito do mouse e desmarque exibir objeto. O que acontece?
12. Construa os segmentos AD e DC. Pegue a ferramenta segmento definido por dois pontos (B2). Clique no ponto A em seguida no ponto D em seguida clique novamente em D e depois em C.
13. Calcule os comprimentos das diagonais do paralelogramo. Pegue a ferramenta distância ou comprimento (B7), clique sobre o ponto A em seguida no Ponto C, observe a medida. Em seguida, com a mesma ferramenta, clique no ponto B e depois no D. Compare as medidas pela janela de álgebra. Existe coincidência, por quê?
14. Calcule também os comprimentos dos lados do paralelogramo. Com a ferramenta distância ou comprimento (B7), clique sobre o ponto A, depois no Ponto B, observe a medida. Em seguida, com a mesma ferramenta, clique no ponto C e depois no D. Compare as medidas pela janela de álgebra. Existe coincidência, por quê? Ainda com a mesma ferramenta, clique no ponto A depois no D, em seguida, no ponto B e depois no ponto C. Compare as medidas pela janela de álgebra. Existe coincidência, por quê?
15. Com a ferramenta mover (B1), clique no ponto A e arraste, observe o que acontece com o ponto E. Faça o mesmo com os pontos B e C.
16. Existe outra forma de determinar o quarto vértice usando algum recurso deste programa?
17. Faça uma investigação: como posso encontrar o quarto vértice utilizando a ferramenta reflexão com relação a um ponto (B8)? Descreva.

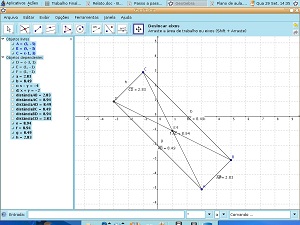
Tela final da construção no GeoGebra



Acesse a imagem ampliada