Relato: Medidas dos ângulos externos não adjacentes de um triângulo

Autor: Maurilio Santos
Instituição: Colégio Estadual Dom Bosco
Município: Campo Mourão
Conteúdo: Medidas dos ângulos externos não adjacentes de um triângulo
Série: 7ª / 8° ano

---

Este material foi elaborado como requisito de avaliação final da oficina Geogebra, sob orientação da docente, assessora pedagógica Giselli Mocelin Martins, da equipe da Coordenação Regional de Tecnologia na Educação do Núcleo Regional de Educação, de Campo Mourão.

Justificativa

A matemática desenvolvida em sala de aula não deve simplesmente ser ditada por nós professores como verdades absolutas, sem possibilitar ao aluno a comprovação dessas verdades.
Nesse sentido, para melhor compreender os conteúdos de Geometria, o aluno pode dispor de materiais manipulativos e de softwares educacionais, como o GeoGebra - recurso utilizado nesta proposta de aula.

Objetivos

Reforçar o conteúdo de soma das medidas dos ângulos internos de um triângulo.

Desenvolvimento metodológico

Inicialmente faça a exposição teórica do conteúdo. Em seguida, aplique as atividades de aprendizagem aos alunos, com a utilização do transferidor, envolvendo uma breve revisão do conteúdo de medida de ângulos. Posteriormente, acompanhe os alunos no desenvolvimento de atividades referentes à construção de triângulos.
Depois, utilizando lápis, régua e transferidor, os alunos construirão triângulos e medirão os ângulos internos registrando os seus valores numa operação de soma, a fim de compreender que cada ângulo externo é igual à soma dos ângulos internos não adjacentes.
Para reforçar o conteúdo, utilize o software GeoGebra para construir um triângulo de vértices móveis e obter suas próprias conclusões a respeito do conteúdo em questão. Para isso, utilize o passo a passo desenvolvido neste plano de aula.

Recursos

Lápis, borracha, régua, lápis de cor, transferidor, caderno, computador com o software GeoGebra instalado.

Avaliação

A avaliação ocorrerá em vários momentos, continuamente, de forma que o professor e o aluno percebam os conhecimentos adquiridos no processo de ensino e aprendizagem; o aluno identifique as suas dificuldades; e o professor, por sua vez, retome o conteúdo num processo de revisão que venha a sanar os déficits de aprendizagem.

Referências

JAKUBOVIC, José; LELLIS, Marcelo. Matemática na medida certa: 7ª série. 3. ed. São Paulo: Scipione, 1998.
PARANÁ. Secretaria de Estado da Educação. Diretrizes Curriculares da a Educação Básica. Matemática. Curitiba: Seed, 2008.


Passo a passo da atividade no software GeoGebra

Propriedade: Em qualquer triângulo, cada ângulo externo é a soma dos ângulos internos não adjacentes.

Atividade: Demonstrar a propriedade e conclui-la de tal forma que o aluno compreenda que em qualquer triângulo cada ângulo externo é a soma dos ângulos internos não adjacentes.

1. Clicar no botão 3 e construir um segmento definido por dois pontos: Segmento AB
2. Clicar no botão 5 e, utilizando a ferramenta Polígono, construir o triângulo ACD.
3. Clicar na extremidade de AB em A em C (exterior ao segmento AB) e D (pertencendo ao segmento AB) e fechar o triângulo em A.
4. Clicar na janela 8 e utilizar a ferramenta Ângulo para medir os ângulos.
5. Registrar no triângulo a medida dos ângulos clicando em DAC, ACD e CDA, nesta ordem. Para registrar a medida do ângulo externo D, clicar em BDA, nesta ordem.
6. Clicar na janela 1 e, na ferramenta Mover, mover o ponto D. Verificar qual a relação que há entre a soma dos ângulos internos não adjacentes e o ângulo externo complementar a D.
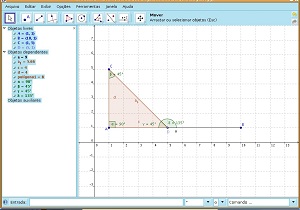
7. Alterar o triângulo ACD para um triângulo retângulo em A. Mover o vértice C até formar um ângulo de 35º e verificar se a relação encontrada anteriormente é válida para este triângulo.