Relato: Geometria analítica - circunferências

Autora: Alzenir Virginia Ferreira Soistak
E-mail: nisoistak@seed.pr.br
Instituição: Colégio Estadual Agrícola Augusto Ribas
Município: Ponta Grossa - PR
Conteúdo: Geometria analítica - circunferências
Série: 3ª Ensino Médio

---

Justificativa

O conteúdo de Geometria analítica é um pouco complexo para os alunos do curso técnico em agropecuária. São poucos os alunos que conseguem relacionar a parte da geometria com a parte algébrica. Muitos acham que não tem utilidade as várias “contas” que são efetuadas e ainda apresentam dificuldades no desenvolvimento algébrico dos cálculos efetuados para analisarem suas respostas.
Com o software GeoGebra, tanto a parte geométrica como a parte algébrica ficam dinâmicas e de fácil compreensão aos alunos que precisam de demonstrações para melhor aprendizagem e compreensão desses conteúdos.

Desenvolvimento metodológico

A duração dessa proposta é de duas aulas de 50 minutos, dependendo do nível de conhecimento e disposição da turma.
Anterior a essa aula, os alunos já devem ter estudado o plano cartesiano e a localização de uma circunferência nesse plano, bem como já devem conhecer a equação da circunferência, seu centro e a medida do raio. Também já devem ter conhecimento dos recursos do software GeoGebra.
Utilizando o software, ao mover livremente duas circunferências, os alunos perceberão as relações existentes entre a distância dos centros das circunferências e as medidas dos seus raios. Essa ação torna dinâmica a aprendizagem e facilita a compreensão das relações entre geometria e álgebra.
Depois de realizada a atividade no laboratório de informática, os alunos poderão ampliar seus conhecimentos com a leitura do livro didático que traz toda a parte teórica das relações experimentadas no GeoGebra.


Procedimentos para a construção no GeoGebra

1. Abrir o software Geogebra e exibir malha e eixos.
2. Selecionar a sexta ferramenta e clicar em Círculo dado centro e raio - o centro será na origem e raio de medida 3.
3. Renomear o ponto A para C1. Para isso, selecionar o ponto A, clicar com o botão direito do mouse, e, em Propriedades, mudar nome.
4. Observar a equação da circunferência formada.
5. Inserir em qualquer lugar um novo ponto na circunferência clicando na segunda ferramenta e selecionando novo ponto.
6. Na terceira ferramenta, clicar em Segmento definido por dois pontos. Os pontos serão o ponto A e o centro da circunferência.
7. Selecionar o segmento e, pressionando o botão direito do mouse, clicar em Propriedades. Renomear o segmento para "raio1". Em Exibir rótulo, selecionar Nome & Valor. Mudar cor e espessura.
8. Para a segunda circunferência, selecionar novamente a sexta ferramenta - círculo definido pelo centro e um dos seus pontos. Ao selecionar com o mouse, o centro será o ponto (4,1) e o ponto (3,2) será nomeado como ponto C.
9. Renomear os pontos surgidos selecionando, primeiramente, o ponto B. Depois, clicando com o botão direito do mouse, mude o nome para C2. Para renomear o ponto C, selecionar o ponto, clicar com o botão direito do mouse e mudar o nome para B.
10. Observar a equação da circunferência formada.
11. Selecionar a terceira ferramenta, Segmento definido por dois pontos, e clicar nos pontos C2 e B.
12. Selecionar o segmento e, pressionando o botão direito do mouse, em Propriedades, renomear o segmento para "raio2", e, em Exibir rótulo, selecionar Nome & Valor. Mudar cor e espessura.
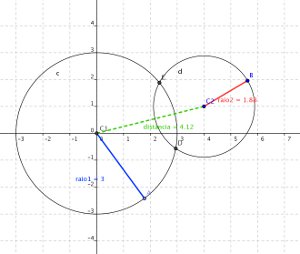
13. Observar como estão as duas circunferências - elas são secantes e possuem dois pontos em comum. Então, selecionar, na segunda ferramenta, Interseção de dois objetos e clicar na circunferência c e d. Os pontos de interseção ficarão destacados como ponto D e E, que só ficará evidente quando as circunferências forem secantes.
14. Selecionar novamente a terceira ferramenta, Segmento definido por dois pontos, e clicar em C1 e C2
15. Renomear o segmento selecionando-o e, pressionando com o botão direito do mouse, clicar em Propriedades e mudar o nome para "distância". Em Exibir rótulo, selecionar Nome & Valor, mudar cor e espessura e estilo de linha para Tracejado.
16. Selecionar a primeira ferramenta, mover e movimentar o ponto B. Para isso, clique nele e, lentamente, leve-o até o ponto (-4,2). Clique e observe o que acontece com o valor do raio da circunferência 2 e os pontos de interseção.
17. Após chegar ao ponto (-4,2), as circunferências passarão a não mais se tocar e os pontos de interseção desaparecerão. Assim a posição das novas circunferências muda: elas não se interceptam internamente.
18. Com a primeira ferramenta selecionada, mover o centro 2 até o centro 1. As circunferências serão concêntricas e a distância será zero.
19. Novamente com a primeira ferramenta selecionada, mover o centro 2 até o ponto (5,0) e o ponto B até as coordenadas (5,1). As circunferências passam a não se interceptar externamente.
20. Novamente com a primeira ferramenta selecionada, mover o ponto B para as coordenadas (5,3). Isso faz com que apareçam os pontos de interseção D e E entre as circunferências.
21. Selecionar a primeira ferramenta e mover, lentamente, o ponto B até as coordenadas (5,2) e observar os valores dos raios e a distancia entre os centros das circunferências. A nova posição entre elas é tangentes externamente.
22. Ainda com a primeira ferramenta selecionada, mover o centro da circunferência 2 para as coordenadas (1,0) e o ponto B para as coordenadas (3,0). A nova posição é tangentes internamente.

Após essas orientações deixar os alunos livremente moverem as circunferências e observarem as posições tomadas por elas, bem como anotarem os valores das distâncias entre seus centros e as relações existentes entre seus raios para cada posição das duas circunferências, pois esses valores e observações serão confrontados com a teoria explicada no livro didático.
Nessa atividade os alunos poderão observar todas as posições relativas de duas circunferências no plano cartesiano, bem como confrontar as relações que indicam tais posições de maneira relativamente simples e interessante.