Relato: Razão áurea

Autora: Ivanice Rodrigues de Lima Bassani
E-mail: ivanicebassani@seed.pr.gov.br
Instituição: Col. Est. Professora Elzira Correia de Sá
Município: Ponta Grossa - PR
Conteúdo: Razão Áurea
Série: 7ª / 8° ano

---

Justificativa

Facilitar o trabalho do professor e tornar a aula de matemática mais atraente para o aluno, é sem dúvida um objetivo a ser alcançado. O uso do computador foi incorporado às ações educativas e o desafio atual é integrar o computador às atividades desenvolvidas na sala de aula, beneficiando a aprendizagem dos estudantes.
Assim, com o software GeoGebra pode-se construir um pentágono regular e com ele mostrar que a razão entre as medidas dos segmentos determinados pelas diagonais que se cruzam é um número irracional misterioso e enigmático, que surge numa infinidade de elementos da natureza: o Número de Ouro.
O número 1,618... foi denominado Número de Ouro ou Número Áureo pelos gregos, que ao estudarem o pentágono regular, descobriram uma razão entre as medidas dos segmentos determinados por diagonais que se interceptam.

Passo a passo para a construção no GeoGebra

1. Abrir o software GeoGebra.
2. No menu Exibir, ocultar os eixos e a malha.
3. Com a ferramenta Polígono regular, construa o pentágono ABCDE.
4. Com Segmento definido por dois pontos, trace todas as diagonais do pentágono.
5. Você poderá observar que se formou uma estrela. Essa figura é conhecida como estrela pentagonal ou pentagrama, e foi adotada por Pitágoras para representar a Irmandade Pitagórica.
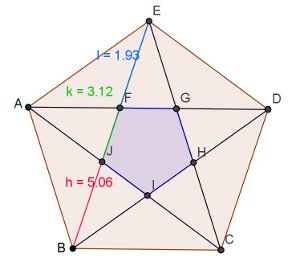
6. Com a ferramenta Novo ponto, marque as intersecções das diagonais. Observe o pentágono menor FGIJ formado. Os gregos ficaram maravilhados com a propagação do pentágono regular: à medida que traçavam as diagonais, obtinham um novo pentágono regular, cujas diagonais mantinham a razão áurea.
7. Para destacar esse pentágono, utilize a ferramenta Polígono e sobreponha sobre ele. Clicando com o botão direito do mouse sobre a figura, em Propriedades / Cor, escolha uma cor e clique em Fechar.
8. Com o botão direito do mouse, clicar em qualquer um dos segmentos (diagonais). Por exemplo: no segmento h, clicar com o botão direito do mouse e, em Propriedades / Básico, na opção Exibir rótulo, selecionar Nome & valor. (Se preferir você também pode trocar a cor).
9. Com a ferramenta Segmento definido por dois pontos, clicar no ponto J e E. No segmento k, clicar com o botão direito do mouse e, em Propriedades / Básico, na opção Exibir rótulo, selecionar Nome & valor. Para finalizar clicar em Fechar.
10. Com Segmento definido por dois pontos, clicar no ponto E e F. Nesse segmento l, clicar com o botão direito do mouse, e, em Propriedades / Básico , na opção Exibir rótulo, selecionar Nome & valor. Para finalizar clicar em Fechar.
11. Pode-se calcular a razão entre os segmentos EB/EJ=EJ/EF=1,616....
12. Valor que se aproxima do número de ouro 1,618...

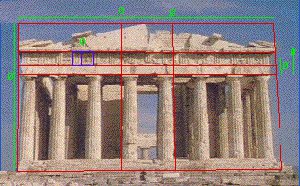
O Partenon Grego, templo representativo do século de Péricles, contém a razão de Ouro no retângulo da fachada (Largura / Altura), o que revela a preocupação de realizar uma obra bela e harmoniosa. O escultor e arquiteto encarregado da construção deste templo foi Fídias. A designação adaptada para o número de ouro é a inicial do nome deste arquiteto - a letra grega f (Phi maiúsculo).