Relato: Função exponencial
Autora: Nilva Nunes de OliveiraInstituição: Colégio Estadual de Campo Mourão
Município: Campo Mourão - PR
Conteúdo: Função exponencial
Série: 1ª do Ensino Médio
Este material foi elaborado como requisito de avaliação final da oficina Geogebra, sob orientação da docente, assessora pedagógica Giselli Mocelin Martins, da equipe da Coordenação Regional de Tecnologia na Educação do Núcleo Regional de Educação, de Campo Mourão.
Justificativa
Os recursos tecnológicos quando usados adequadamente despertam o interesse dos alunos e facilitam a aprendizagem. Sabe-se que nos dias de hoje não é suficiente que os alunos organizem conteúdos, memorizem regras ou repitam modelos, é preciso que o professor oportunize momentos de aprendizagem por meio de tecnologias variadas para que os estudantes se tornem capazes de compreender e lidar com essas tecnologias para resolver situações-problema diversificadas.Nesse sentido é que propomos, nesta atividade, o trabalho com função exponencial utilizando o software GeoGebra.
Por meio desse software, é possível estudar a função exponencial com maior agilidade e melhor visualização, proporcionando aos educandos o estudo de conteúdos com um recurso tecnológico que torna a aprendizagem prazerosa e significativa.
Objetivos
- Ler e interpretar enunciados relacionando-os à utilização de funções matemáticas.
- Reconhecer a função exponencial.
- Construir e analisar gráficos de funções exponenciais.
- Resolver problemas aplicando o conceito de função exponencial.
Desenvolvimento metodológico
Em sala de aula o professor irá retomar o estudo das propriedades das potências para, em seguida, trabalhar com os alunos o conceito de função exponencial, incluindo confecção, leitura e interpretação de gráficos.Nesse estudo, é importante destacar para os alunos que uma função f(x) = ax, em que a é constante positiva e diferente de 1, denomina-se função exponencial.
Por meio de cálculos e construções de gráficos, os alunos vão descobrir quando a função será crescente ou decrescente. É necessário que concluam que a base a tem que ser maior que 1 para que a função seja crescente, e menor que 1 para que seja decrescente.
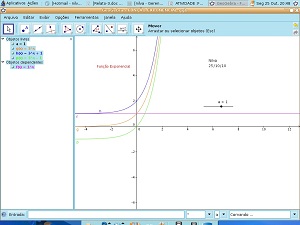
Proponha a atividade de construção do gráfico da função exponencial com o software GeoGebra,
Recursos
Lápis, borracha, régua, caderno, papel milimetrado, computador com o software GeoGebra instalado.Referências
PARANÁ. Secretaria de Estado da Educação. Diretrizes Curriculares da Educação Básica. Matemática. Curitiba: Seed, 2008.SOARES, Elisabeth. Matemática: de olho no mundo do trabalho. Volume único para o Ensino Médio. São Paulo: Scipione, 2005.
Passo a passo para a construção dos gráficos no GeoGebra
- Abra o software GeoGebra.
- Clique no menu Arquivo e selecione Gravar como. Digite o nome do arquivo: funcao_exponencial.
- Selecione a ferramenta Inserir texto e clique onde deseja que o texto apareça na área de trabalho. Digite seu nome. Tecle Enter. Digite a data e clique em Aplicar.
- Selecione a ferramenta Inserir texto e clique onde deseja que o título da atividade apareça na área de trabalho. Digite "Função exponencial" e clique em Aplicar.
- Na janela geométrica, insira um seletor, denominado a com variação [-5,5].
- Digite no campo de entrada a função f(x)=a^x
- Mova o parâmetro a e observe atentamente o que acontece com o gráfico construído.
- O que ocorre quando você varia o valor de a? Por quê?
- O que acontece com a sua função quando o parâmetro a é 1?
- É possível que o gráfico de uma função exponencial passe por todos os quadrantes? Por quê?
- Para quais valores de a a função exponencial é crescente? E decrescente?
- Construa gráfico da função y=3^x. Com base nele, faça os gráficos das funções y=3^x+1 e y=3^x-1, num mesmo plano cartesiano. Que diferenças pode ser observadas entre os três gráficos?
Construção no GeoGebra