Relato: Soma dos ângulos internos de um triângulo

Autora: Alessandra Guizelini
E-mail: alleguizelini@gmail.com
Instituição: Colégio Estadual Padre José Canale
Município: Apucarana
Conteúdo: Soma dos ângulos internos de um triângulo
Série: 7ª / 8° ano

---

Justificativa

Com o uso do software GeoGebra, o ensino da soma dos ângulos internos de um triângulo torna-se mais dinâmico e eficaz. Considerando que o aluno já esteja familiarizado com o software, em pouco tempo ele pode construir diversos triângulos diferentes, medir seus ângulos internos e verificar que a soma é sempre a mesma. Antes, construções com régua e transferidor, dificultava o trabalho com medidas de ângulos, quando esses não eram números inteiros. Hoje, com o GeoGebra essa dificuldade foi superada: tornou-se mais ágil a parte da construção do triângulo e da medição dos ângulos, possibilitando ao aluno concentrar-se mais na obtenção e observação do resultado da soma dos ângulos internos de um triângulo e sua regularidade.

Objetivos

• Identificar e somar os ângulos internos de triângulos.
• Perceber que a soma dos ângulos internos de um triângulo é sempre a mesma para qualquer triângulo e independe da medida da área e do perímetro desse triângulo.

Abordagem pedagógica

Na Matemática, o estudo da soma dos ângulos internos do triângulo tem sua importância justificada pelo fato de que a soma dos ângulos de qualquer outro polígono surge a partir da divisão deste em triângulos pelas diagonais de um de seus vértices. É possível verificar esse fato a partir de desenhos com régua e transferidor, porém esta é uma tarefa demorada e muitas vezes cansativa para a maioria dos alunos. Os conceitos difundidos pela Educação Matemática apontam para a necessidade de dinamizar mais do que mecanizar o estudo dos conteúdos. Assim, esta atividade propõe justamente a isso: que o aluno se concentre mais na percepção das características dos triângulos que constrói e na regularidade da soma de ângulos internos, primeiro passo fundamental para a dedução da fórmula da soma dos ângulos internos de um polígono.

Metodologia

Será utilizado o software GeoGebra para a construção de triângulos e obtenção das respectivas medidas da área, do comprimento dos lados e dos ângulos.
A ambientação dos alunos com o software e suas ferramentas já deve ter sido feita anteriormente.
Será entregue aos alunos uma cópia da atividade a ser desenvolvida por eles, em grupos, utilizando o GeoGebra.

Atividade
Utilizando a ferramenta Polígono, construa um triângulo ABC.
Utilizando a ferramenta Área, determinar a medida da área do triângulo ABC.
Utilizando a ferramenta Distância ou comprimento, determinar a medida dos lados AB, BC e AC do triângulo ABC.
Utilizando a ferramenta Ângulo, determinar a medida dos ângulos A, B e C.




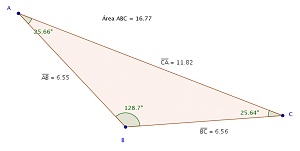
Figura 1 - Exemplo de triângulo ABC - 1ª etapa

Acesse imagem ampliada

Completar a tabela, na linha correspondente a 1ª etapa, com as medidas da área, dos lados e dos ângulos do triângulo ABC construído no GeoGebra, bem como com as somas dos lados e dos ângulos.

Tabela para preencher



Acesse imagem ampliada


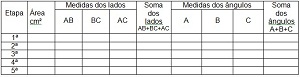
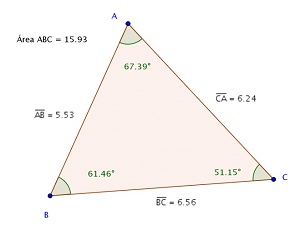
Figura 2 - Exemplo de triângulo ABC modificado - 2ª etapa

Acesse imagem ampliada


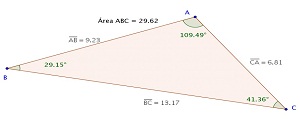
Figura 3 - Exemplo de triângulo ABC modificado - 3ª etapa

Acesse imagem ampliada


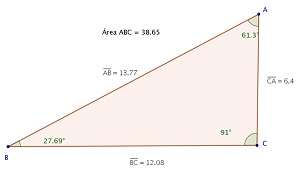
Figura 4 - Exemplo de triângulo ABC modificado - 4ª etapa

Acesse imagem ampliada


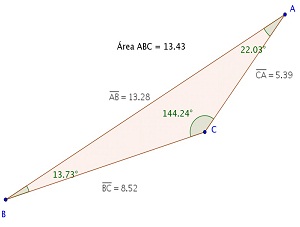
Figura 5 - Exemplo de triângulo ABC modificado - 5ª etapa

Acesse imagem ampliada

Utilizando a ferramenta Mover, movimente um, dois ou os três pontos correspondentes aos vértices do triângulo ABC, obtendo quatro outros triângulos. Para cada triângulo obtido, complete uma linha da tabela (2ª, 3ª, 4ª e 5ª etapas).

Exemplo de tabela após preenchimento



Acesse imagem ampliada

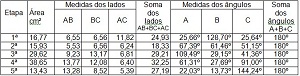
Propor aos alunos a discussão da seguinte questão: O que podemos concluir observando as informações da tabela?
Conduzir a discussão a respeito das medidas expressas na tabela para a seguinte conclusão: a soma dos ângulos internos de qualquer triângulo é igual a 180º.

Período de realização da atividade: 2 horas/aula

Avaliação

A aprendizagem dos alunos será avaliada oralmente durante as discussões e por escrito pela observação da folha de atividades realizadas por eles, tendo em vista os objetivos propostos para a aula.

Referências

ANDRINI, A.; VASCONCELLOS, M. J. Novo Praticando Matemática - 7ª série. São Paulo: Editora do Brasil, 2002.
BONJORNO, J. R.; BONJORNO, R. A.; OLIVARES, A. Matemática: fazendo a diferença. São Paulo: FTD, 2006.
PARANÁ. Secretaria de Estado da Educação. Diretrizes Curriculares da Educação Básica. Curitiba: Seed, 2008.