Relato: Triângulos
Autora: Ivane Marcarini SimionatoE-mail: ivanes@seed.pr.gov.br
Instituição: Colégio Estadual Carlos Gomes - EFM
Município: Pato Branco - PR
Conteúdo: Triângulos
Série: 7ª / 8º ano
Este material foi elaborado como requisito de avaliação final da oficina Geogebra, sob orientação do docente, acessor Ivonei Almeida, da equipe da Coordenação Regional de Tecnologia Educacional do Núcleo Regional de Pato Branco.
Justificativa
O estudo do triângulo e seus elementos é conteúdo programático desta série, e, portanto, tornasse necessário trabalhá-lo de forma criativa e eficaz devido à sua grande utilização na engenharia, arquitetura e também por estar presente num grande número de objetos ao nosso redor.
A forma triangular é usada desde a antiguidade para tornar as construções mais rígidas e seguras, pois essa forma permite descarregar grandes pressões exercidas por grandes pesos. Encontramos a forma triangular na construção de pontes e túmulos antigos. Os gregos o usavam para construir, por exemplo, portas de igrejas. Hoje é utilizado na cobertura de estádios, torres de alta tensão (para suportar ventos fortes), e na construção civil em geral.
Estudar os pontos notáveis do triângulo permite compreender melhor o porquê da sua utilização na vida cotidiana.
Objetivos
- Construir os diferentes tipos de triângulos.
- Medir e classificar os triângulos quanto aos ângulos e quanto aos lados.
- Encontrar pontos notáveis de um triângulo ABC, o Ortocentro, o Baricentro e o Incentro, utilizando o software GeoGebra.
Encaminhamento metodológico e recursos didáticos
Primeiramente, na sala de aula, apresentar as definições dos tipos de triângulos, classificação, pontos notáveis do triângulo e imagens, retidas da Internet, que representem o baricentro, o circuncentro, o ortocentro e o incentro de um triângulo, usando para isso a TV Multimídia. Em seguida, no laboratório de informática, utilizar o software GeoGebra para construir, diferenciar e classificar os triângulos. Determinar os pontos notáveis citados anteriormente, com base nos procedimentos apresentados em anexo.
Finalizar as atividades com a discussão e análise dos resultados encontrados.
Avaliação
Os estudantes serão avaliados considerando-se a sua participação, resolução correta das atividades e envolvimento na busca de respostas para as situações-problema apresentadas.
Referências
GIOVANNI, José Ruy; GIOVANNI JR., José Ruy. Matemática: pensar e descobrir. São Paulo: FTD, 2002.
IMENES, Luiz Márcio. Formas geométricas: conversa de professor de matemática. 1996.
MEDEIROS, C. F. Por uma educação matemática como intersubjetividade. In: BICUDO, M. V. Educação matemática. São Paulo: Cortez, 1987.
PARANÁ. Secretaria de Estado da Educação. Diretrizes Curriculares para a Educação Básica. Matemática. Curitiba: Seed, 2007.
Atividades - Classificação dos triângulos quanto aos lados e ângulos
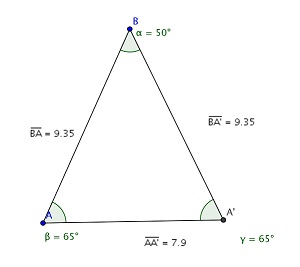
1 - Triângulo isósceles
a) Abra o GeoGebra usando o aplicativo Educação. Clique em Matemática, depois GeoGebra.
b) Explorando a ferramenta Ângulo, crie um triângulo isósceles com ângulo de 50º e lados paralelos medindo 3 u.m.
c) Ainda usando a ferramenta Ângulo, meça os ângulos e faça o comparativo entre eles.
d) Usando a ferramenta de medida, meça os lados do triângulo, compare e veja o que aconteceu.
e) Usando a ferramenta Mover, mova as medidas para fora da figura.
f) Movimente o triângulo a partir de seus vértices e veja o que acontece. Ele perde sua forma inicial? Os ângulos sofrem modificação?
g) Esse triângulo é acutângulo, obtusângulo ou retângulo?
h) Encontre a altura do triangulo utilizando a ferramenta Ponto médio e depois Perpendicular.
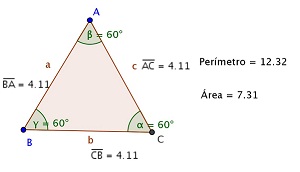
Acesse imagem ampliada2) Triângulo equilátero
a) Explorando a ferramenta Polígono regular, crie um triângulo equilátero com 3 u.m de lado.
b) Usando a ferramenta Ângulo, meça os ângulos e faça o comparativo entre eles.
c) Utilizando a ferramenta de medida, meça os lados do triângulo, compare e veja o que aconteceu.
d) Usando a ferramenta cm, encontre o perímetro do triângulo.
e) Usando a ferramenta cm², determine a área do triângulo.
f) Com a ferramenta Mover, mova as medidas para fora da figura.
e) Movimente o triângulo a partir de seus vértices e veja o que acontece. Ele perde sua forma inicial? Os ângulos sofrem modificação?
g) Esse triângulo é acutângulo, obtusângulo ou retângulo?
h) Quanto mede a altura desse triângulo? (Sugestão: encontre a altura por meio das ferramentas Ponto médio e Perpendicular. Então, usando a ferramenta cm, meça).
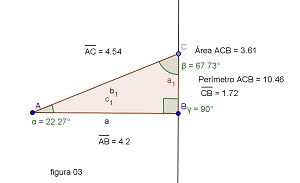
Acesse imagem ampliada3) Triângulo escaleno
a) Explorando as ferramentas Segmento de reta e Reta perpendicular, crie um triângulo escaleno retângulo.
b) Com a ferramenta Ângulo, meça os ângulos e faça o comparativo entre eles.
c) Utilizando a ferramenta de medida, meça os lados do triângulo, compare e veja o que aconteceu.
d) Com a ferramenta Polígono, ligue os pontos. Pinte a figura.
e) Usando a ferramenta cm, encontre o perímetro do triângulo.
f) Usando a ferramenta cm², determine a área do triângulo.
g) Usando a ferramenta Mover, mova as medidas para fora da figura.
h) Movimente o triângulo a partir de seus vértices e veja o que acontece. Ele perde sua forma inicial? Os ângulos sofrem modificação?
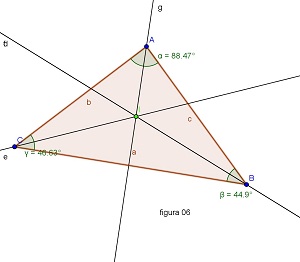
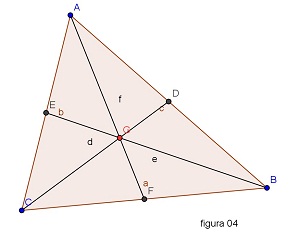
Acesse imagem ampliada4) Baricentro de um triângulo
a) Utilizando as ferramentas conhecidas, construa um triângulo qualquer.
b) Trace a mediana relativa a cada um dos lados, usando as ferramentas Ponto médio e Segmento.
c) Localize o baricentro e mude sua cor.
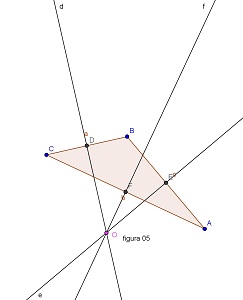
Acesse imagem ampliada5) Ortocentro de um triângulo
a) Construa um triângulo usando a ferramenta Polígonos.
b) Trace as alturas utilizando as ferramentas Ponto médio e Perpendicular.
c) Localize o encontro das alturas com a ferramenta Intersecção.
d) Renomeie o ponto G para ponto O e modifique a cor.
e) Movimente o triângulo usando a ferramenta Mover. Verifique o que ocorre.
Acesse imagem ampliada6) Incentro de um triângulo
a) Construa um triângulo utllizando a ferramenta Polígonos.
b) Trace a bissetriz de cada ângulo usando a ferramenta Bissetriz de um ângulo.
c) Localize o encontro das bissetrizes com a ferramenta Intersecção.
d) Renomeie o ponto G para ponto I e modifique a cor.
e) Movimente o triângulo usando a ferramenta Mover. Observe o que ocorre.
Acesse imagem ampliada
