Relato: Trigonometria

Autora: Mariza Antoninha Secco
E-mail: iza.secco@hotmail.com
Instituição: Colégio Estadual de Pato Branco - EFMPEN
Município: Branco - PR
Conteúdo: Trigonometria
Série: 1ª do Ensino Médio

---

Este material foi elaborado como requisito de avaliação final da oficina Geogebra, sob orientação do docente, acessor pedagógico Ivonei Almeida, da equipe da Coordenação Regional de Tecnologia Educacional do Núcleo Regional, de Pato Branco.

Justificativa

A necessidade de medir é quase tão antiga quanto a necessidade de contar. Desde as primeiras civilizações, as medidas se tornaram a linguagem fundamental à realização dos negócios no mundo do comércio. A trigonometria, sendo conteúdo específico de grandezas e medidas, contempla as relações entre as medidas dos lados e dos ângulos de um triângulo, relações essas desenvolvidas a partir da necessidade do homem determinar, por exemplo, medidas inacessíveis. A trigonometria tem grande aplicação dentro de outras áreas, como é o caso da Astronomia e da Física.

Objetivo

• Construir o ciclo trigonométrico para que os educandos descubram e compreendam, através de atividades investigativas, os valores de seno, cosseno e tangente dos ângulos da 1ª volta da circunferência, utilizando o software GeoGebra.

Encaminhamento metodológico e recursos didáticos

Primeiramente, na sala de aula e laboratório de informática, utilizando o software GeoGebra, trabalhe com a compreensão e aplicação das relações trigonométricas no triângulo retângulo. Após a compreensão e o domínio, utilizando a trigonometria no triângulo, novamente no laboratório de informática, construa o ciclo trigonométrico para que compreendam a trigonometria da circunferência - apresente primeiramente as relações de seno e cosseno e posteriormente a tangente.
Em um segundo momento, descreva as atividades propostas realizando uma constante discussão com os alunos para que eles construam o seu conhecimento e atinjam os objetivos a que será proposto.
Utilize para comparações nas atividades investigativas a tabela de valores dos senos, cossenos e tangentes dos ângulos do 1º quadrante e a calculadora cientifica para os ângulos dos demais quadrantes. A tabela de valores dos senos, cossenos e tangentes pode ser encontrada em materiais didáticos diversos.

Avaliação

Participação e envolvimento dos alunos no desenvolvimento das atividades propostas.

Referências

DANTE, Luiz Roberto. Matemática. São Paulo: Ática, 2005. v. único.
GUELLI, Oscar. Dando corda na trigonometria. São Paulo: Ática, 1999. (Coleção Contando a História da Matemática)
PARANÁ. Secretaria de Estado da Educação. Diretrizes Curriculares para a Educação Básica. Matemática. Curitiba: Seed, 2007.


Atividade 1: Construindo o ciclo trigonométrico

a) Abrir o software GeoGebra, clicar no ícone Seletor e em um ponto na tela. Na caixa de diálogo que se abrirá, escolher a opção Ângulo e clicar em Aplicar.
b) Digite na tela inicial o ponto A=(0,0) e tecle Enter.
c) Escolha a opção Círculo dados centro e raio, clique no ponto A e digite, na janela que se abrirá, o valor 1. Clique em OK.
d) Na tela de entrada, digite o ponto B=(1,0).
e) No ícone Ângulo, selecione Ângulo com amplitude fixa. Clique no ponto B e no ponto A, nessa sequência. Na caixa de diálogo que se abrirá, digite ?. Aparecerá o valor do ângulo e será criado o ponto B’ na circunferência (caso o valor do ângulo seja muito pequeno e de difícil visualização, em Mover, mova o seletor aumentando seu valor).
f) Escolha a opção Reta definida por dois pontos. Clique no ponto A e no B’.
g) No ícone Selecionar reta perpendicular, clique no ponto B’ e no eixo x. No ícone Intersecção de dois objetos, clique sobre a reta e o eixo x; será criado o ponto C sobre o eixo x. Depois, clique na reta perpendicular ao eixo x com o botão direito do mouse. Na janela que será aberta, clique em Exibir objeto (a reta desaparecerá). No ícone Selecionar segmento definido por dois pontos, clique nos pontos B’ e C. Depois, clique com o botão direito do mouse sobre o segmento B’C. Na janela que se abrirá, selecione Propriedades / Estilo. Em Estilo das retas, selecione Pontilhado e, em Cor, mude a sua cor.
h) No ícone Selecionar reta perpendicular, clique no ponto B’ e eixo y. No ícone Intersecção de dois objetos, clique sobre a reta e o eixo y. Será criado o ponto D sobre o eixo y. Para fazer o segmento B’D e pontilhar, siga os mesmos passos anteriores.
Está construído o ciclo trigonométrico para observar os valores de seno e cosseno dos ângulos.



Acesse imagem ampliada

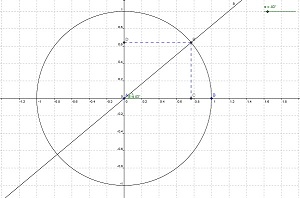
Obs.: Caso a malha não esteja aparecendo, para uma melhor visualização e compreensão dos valores das coordenadas x e y, em Exibir malhar, clique na opção Ampliar e ajuste a malha até que os valores nos eixos apareçam divididos de 0,2 em 0,2. Caso haja necessidade de centralização dos eixos, ajuste com a opção Deslocar eixos. Para trabalharmos com mais precisão dos dados, com a ferramenta Arredondamento, clique em 3 casas decimais.

Atividade 2: Descobrindo os valores de seno e cosseno dos ângulos a partir da circunferência trigonométrica criada

a) Mova o seletor livremente e veja o que acontece com os valores do ponto B’ e do ângulo ?.
Sugestão: com o seletor selecionado, use as setas do teclado para mover o ponto B’ e ter um determinado valor do ângulo ?.
b) Mova o seletor apenas no 1º quadrante para analisar e responder as questões:
1) Escolha o valor de um ângulo e observe o valor da abscissa (valor de x) do ponto B’, compare esses valores com os valores da tabela fornecida dos senos, cossenos e tangentes. O que você conclui?
2) Escolha outro valor para o ângulo. Faça a mesma observação do item anterior. A conclusão é a mesma?
- Repita esses procedimentos várias vezes, sempre observando esses itens já mencionados anteriormente. Veja se a conclusão é sempre a mesma.
3) Escolha o valor de um ângulo e observe o valor da ordenada (valor de y) do ponto B’, compare esses valores com os valores da tabela fornecida dos senos, cossenos e tangentes. O que você conclui?
4) Escolha outro valor para o ângulo. Faça a mesma observação do item anterior. A conclusão é a mesma? Repita esses procedimentos várias vezes, sempre observando esses itens já mencionados anteriormente. Veja se a conclusão é sempre a mesma.
c) Nessa atividade, mova o seletor nos demais quadrante e com auxilio da calculadora cientifica analise e responda:
1) As conclusões feitas para os valores do seno e do cosseno do ângulo ? são válidas para esses outros quadrantes?
2) Escreva as coordenadas do ponto B’ aplicando a correspondência do seno e do cosseno em relação à sua abscissa e sua ordenada.
3) Com base no que você já aprendeu na trigonometria do triângulo retângulo, encontre uma justificativa matemática ou comprovação para:
• O valor do cosseno de ? é o valor da abscissa do ponto B’.
• O valor do seno de ? é o valor da ordenada do ponto B’.

Atividade 3: Construindo a reta tangente ao ciclo trigonométrico

a) No ciclo trigonométrico já construído vamos desenhar uma reta tangente à circunferência passando pelo ponto B. Para isso escolha a opção Reta perpendicular e clique no ponto B e no eixo x.
b) Na opção Intersecção de dois objetos, clique na intersecção entre as duas retas formadas. Será criado o ponto E.
c) Selecione Reta perpendicular e clique no ponto E e no eixo y. No ícone Intersecção de dois objetos, clique sobre a reta e o eixo y; será criado ponto F sobre o eixo y. Para fazer o segmento EF e pontilhar, siga os mesmos passos realizados na construção dos segmentos anteriores.




Acesse imagem ampliada

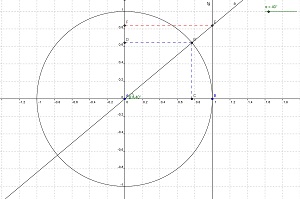
Atividade 4: Descobrindo os valores da tangente dos ângulos

a) Mova livremente o seletor e verifique o que acontece em relação ao ângulo ? e o ponto E.
b) Nessa atividade, mova o seletor apenas no 1º quadrante para analisar e responder as questões:
1) Escolha o valor de um ângulo e observe o valor da ordenada (valor de y) do ponto E. Compare esses valores com os valores da tabela fornecida dos senos, cossenos e tangentes. O que você conclui?
2) Escolha outro valor para o ângulo. Faça a mesma observação do item anterior. A conclusão é a mesma?
- Repita esses procedimentos várias vezes, sempre observando esses itens já mencionados anteriormente. Veja se a conclusão é sempre a mesma.
3) Use o valor do ângulo 90° e observe o que acontece com o ponto E. Qual a explicação para indefinido? Por que?
c) Nessa atividade, mova o seletor nos demais quadrante e, com auxilio da calculadora cientifica, analise e responda as questões:
1) As conclusões feitas para os valores da tangente do ângulo ? são válidas para esses outros quadrantes?
2) Use o valor do ângulo 270° e observe o que acontece com o ponto E. Podemos chegar a mesma conclusão feita em relação ao ângulo de 90°?
3) Com base no que você já aprendeu na trigonometria do triângulo retângulo, encontre uma justificativa matemática ou comprovação para:
• O valor da tangente de ? é o valor da ordenada do ponto E.

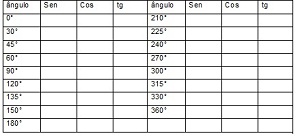
Organizando os dados

1) Com o uso do ciclo trigonométrico construido, verifique e escreva na tabela a seguir o valor do seno, do cosseno e da tangente dos ângulos solicitados:


Acesse imagem ampliada