Relato: Introdução à trigonometria
Autora: Marize Cossa PereiraE-mail: marizecp@hotmail.com
Instituição: Colégio Estadual de Pato Branco
Município: Pato Branco – PR
Conteúdo: Introdução à Trigonometria
Série: 8ª série / 9º ano
Este material foi elaborado como requisito de avaliação final da oficina GeoGebra, sob orientação do docente, assessor pedagógico Ivonei Almeida, da equipe da Coordenação Regional de Tecnologia Educacional do Núcleo Regional de Pato Branco.
Justificativa
No ensino da Matemática é indispensável que haja relação entre os conteúdos curriculares e a resolução de problemas. As noções de seno, cosseno e tangente serão apresentadas de maneira que possam resolver uma situação problemática e ao mesmo tempo, fazer com que o aluno perceba que as razões trigonométricas são relações existentes entre as medidas dos lados de um triângulo retângulo.
As relações serão trabalhadas a partir da semelhança de triângulos no software GeoGebra, onde será desenhado um triângulo retângulo e movimentados os seus lados para que alterem suas medidas, provando que as razões entre os lados permanecerão iguais, e movimentado seus ângulos para que sejam calculadas as razões em triângulos variados, formando uma parte da tabela trigonométrica.
Objetivos
- Identificar as razões trigonométricas (seno, cosseno e tangente) no triângulo retângulo como razão de semelhança.
- Aplicar as razões trigonométricas para determinar elementos desconhecidos no triângulo retângulo.
1) Abrir o software GeoGebra.
2) Criar um seletor de intervalo 1 a 10.
3) Criar outro seletor para o ângulo de intervalo 1° a 89°.
4) Clicar no ícone Segmento com comprimento fixo, digitar a letra “a” no seletor e aplicar.
5) Clicar em Ângulo com amplitude fixa no B e no A, digitar “?” no seletor e aplicar.
6) Traçar uma perpendicular passando por B.
7) Traçar uma “reta passando por dois pontos” (no A e no B’).
8) Fazer a intersecção entre as retas para criar o ponto C.
9) Com o ícone Polígono, desenhar o triângulo retângulo.
10) Excluir as retas, as letras, os pontos que sobram, deixando apenas os pontos A, B, C, clicando com o botão direito do mouse sobre o que se quer esconder (rótulo e objeto).
11) Com o ícone Ângulo, medir o ângulo ACB.
12) Com o ícone Distância, colocar as medidas dos três lados do triângulo.
Atividade 1
a) Com o ícone Mover no primeiro seletor, movimente livremente e analise o que acontece.
b) Com o ícone Mover no segundo seletor, movimente livremente e analise o que acontece.
c) Deixe o triângulo com as medidas de 20° e 70°.
d) Usando a calculadora, encontre a razão entre os segmentos: BC e AC; AB e AC; BC e AB, anotando os resultados.
e) Movimente o primeiro seletor (a) encontrando um triângulo semelhante, com medidas maiores e repita os cálculos entre os segmentos.
f) Repita o procedimento tantas vezes quantas forem necessárias.
g) Movimente o segundo seletor (do ângulo) e deixe na medida de 30º, repetindo as operações entre os segmentos. Mude o tamanho dos lados e repita a operação.
h) Realizar esse procedimento com vários ângulos e tamanhos de triângulos.
i) O que podemos perceber?
Os alunos deverão perceber que não importa o tamanho dos lados, desde que o ângulo permaneça o mesmo, as razões serão iguais.
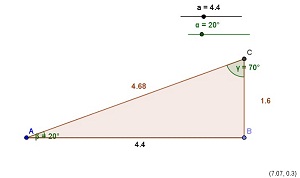
A partir dessa experiência, nomear as razões entre os catetos e a hipotenusa, apresentando o seno como a razão entre o cateto oposto ao ângulo pela hipotenusa; o cosseno, como a razão entre o cateto adjacente e a hipotenusa; e a tangente, como a razão entre o cateto oposto e o adjacente; e ainda, a tabela trigonométrica.
Mostrar que os resultados obtidos pelos alunos já foram encontrados há muito tempo, com a finalidade de resolver problemas práticos relacionados à navegação e à Astronomia, e até hoje são utilizados, principalmente, por astrônomos e agrimensores, para medir distâncias muito grandes ou de difícil acesso, como medir largura de um rio, altura de uma montanha, etc.
Atividade 2
Resolver o problema: Um avião decola do aeroporto (A) e sobe segundo um ângulo constante de 15º com a horizontal. Na direção do percurso do avião, a 2 Km do aeroporto, existe uma torre retransmissora de televisão de 40 m de altura. Verifique se existe a possibilidade de o avião se chocar com a torre. (Nesse caso, ele deveria desviar-se da rota)
Resolução
Representar a situação através do desenho a seguir.
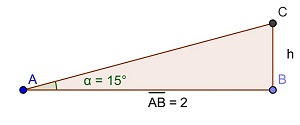
Procedimento
a) Traçar um segmento de reta com comprimento fixo e colocar medida 2 (representando 2 Km).
b) Clicar em Ângulo com amplitude fixa do B para A e colocar 15º.
c) Traçar a semirreta passando por dois pontos, A e B’.
d) Traçar uma perpendicular passando por B.
e) Fazer a intersecção entre a perpendicular e a semirreta para encontrar o ponto C.
f) Desenhar o triângulo pelos pontos A, B, C.
g) Excluir, com o botão direito do mouse, os rótulos e os objetos, deixando apenas o triângulo ABC.
h) Medir o segmento AB (2).
i) Inserir texto para representar a altura BC (h).
Tendo o desenho pronto, questionar para descobrir qual das três razões deverá ser usada para descobrir a medida h da altura. (no caso a tangente)
Procurar na tabela o valor da tangente de 15º (0,27) e efetuar o cálculo:
tg 15º = h/2
0,27 = h/2
h = 540 m
Verificar no desenho, medindo o segmento BC (0,54)
Portanto, o avião poderá seguir sua rota, pois não vai se chocar com a torre.
Referências

