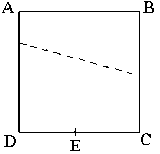
Solução do Problema A Dobradura

Este problema foi resolvido por: - Eliane Grunow Kuipers - Col. Est. Julia Wanderley - Carambeí - PR - Denis dos Santos Machado - IPE - São José dos Pinhais - PR - Valéria do Rocio Pedroso Walchaki - Col. Linda Bacila - Ponta Grossa - PR Parabéns!

Solução enviada por Eliane Grunow Kuipers: Traçamos no centro do quadrado ABCD os eixos x e y e obtemos os vértices de coordenadas A(-4;4); B(4;4); C(4;-4); D(-4;-4) e E(0; -4), considerando que o quadrado tem 8cm de lado. Unindo o vértice B ao ponto E obtemos um ponto médio de coordenadas (2;0) e da mesma forma, unindo o vértice A ao ponto E, obtemos o ponto médio de coordenadas (-2;0). A seguir obtemos a equação da reta que passa pelos pontos B e E, sendo r:2x-y-4=0 e determinamos a equação da reta que passa por (2;0) e que é perpendicular a r. Obtemos então a equação t: x+2y-2=0. Semelhantemente determinamos a equação da reta que passa por A e E, s: 2x+y+4=0 que é perpendicular a u: x-2y+2=0, passando por (-2;0).
Determinamos o ponto de intersecção das retas t e u, F(0;1), e considerando que o centro do quadrado está na origem do sistema cartesiano , a distância do ponto F ao centro do quadrado será de 1cm.

Solução enviada por Denis dos Santos Machado: 1°. passo: feitas as dobras informadas na situação-problema se obteve o ponto x. 2°. passo: a folha foi dobrada em 4 partes iguais (2cm cada uma) e se observou que o ponto x ocupou exatamente o ponto medio da altura de uma parte dessas 4. divide 8/4=2, portanto o ponto x está 1cm acima do ponto central da folha.

---

Conheça outros desafios publicados