Solução do Problema Triângulo Acutângulo
Este é um maravilhoso quebra-cabeça geométrico sem conteúdo definido, perfeito para cálculos simples e para qualquer idade… se você ainda não o resolveu, faça uma tentativa antes de olhar a solução! |
SOLUÇÃO
I - Um triângulo acutângulo "original" não precisa que seus ângulos se dividam mais. O diagrama abaixo mostra a divisão padrão em 4 triângulos menores.
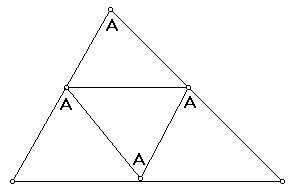
Cada ponto de "junção" nos lados do triângulo original precisa ter os vértices de três triângulos, para evitar o aparecimento de ângulos obtusos.
II - Todavia, todo triângulo obtusângulo "original" precisa que seu ângulo obtuso seja dividido por alguma linha "divisora".
O final desse divisor precisar estar ou do lado oposto, ou em algum lugar no interior do triângulo.
Não pode ser do lado oposto sem se criar outro triângulo obtusângulo - seja à esquerda ou à direito do divisor. E depois você precisa dividir esse ângulo, e assim por diante.
Então precisa haver um ponto interno em que essa linha divisora termine - o ponto B, abaixo:
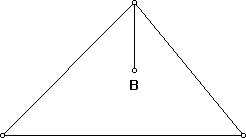
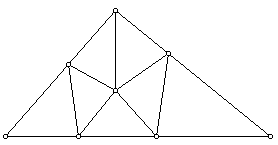
Agora, é preciso ter pelo menos 4 linhas radiais a mais partindo de B - para garantir que nenhum ângulo seja maior do que 90º.
Isso significa um para cada um dos dois lados, e dois para o terceiro lado. O quadro se completa da forma mostrada abaixo:
Conheça outros desafios publicados
 |
 |
 |
 |
 |
 |

