Sugestão de atividade - Permutação - Pintura de bandeiras retangulares com três listras
O objetivo desta atividade é construir a árvore de possibilidades e utilizá-la na elaboração do conceito de permutação simples.
Faça os questionamentos a seguir e peça aos alunos para colocarem na folha com o desenho das bandeiras o número de cada item e pintarem a quantidade necessária para satisfazer as condições dadas, utilizando apenas as cores verde, amarela e azul.
a). Quantas bandeiras de uma única cor podemos construir?
b). Quantas bandeiras com duas cores diferentes podemos pintar?
c). Quantas bandeiras com três cores diferentes podemos criar?
d). E se não houvesse bandeiras para pintar? Represente a situação da letra c utilizando a árvore de possibilidades.
e). A partir da representação feita na letra d, responda:
e.1). Quantas cores podem ser pintadas na primeira listra?
e.2). Após a pintura da primeira, quantas cores podem ser pintadas na segunda listra?
e.3). Já na terceira listra, podemos contar com quantas cores?
e.4). Como você pode relacionar estes resultados com o número de bandeiras obtidas?
Reserve um tempo para a exploração da atividade;
Após o término do tempo previsto, debata as soluções com a turma.
Nota: Todas as definições e soluções desta aula encontram-se disponíveis em http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/AnaComb.pdf . Portanto, previamente, imprima, faça cópias e distribua.
Imagem da autora
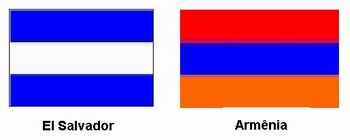
Observação: Deixe claro para todos que é também possível pintar a bandeira com apenas uma ou duas cores. Exiba com o uso do Data Show a figura abaixo como exemplos de bandeiras pintadas com apenas duas cores, para facilitar a compreensão desta observação.
Imagem editada pela autora a partir de http://www.sogeografia.com.br/Bandeiras/Africa/
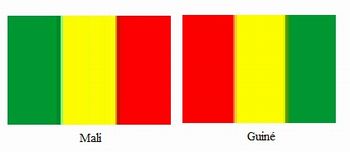
Na letra c, ressalte que a ordem na qual pintamos as listras implica bandeiras diferentes. Exiba o exemplo abaixo, no qual as bandeiras de dois países do continente africano diferem apenas pela ordem das cores. Também vale observar que há, como referência, a posição na qual a bandeira é presa ao mastro.
Imagem editada pela autora a partir de http://www.sogeografia.com.br/Bandeiras/Africa/
Na letra d, a turma deve construir a árvore de possibilidades, já na letra e os alunos devem perceber que o número de bandeiras de n listras que devem ser coloridas com n cores diferentes é dado por n!.
Conte para a turma que este exemplo trata-se de um caso de Permutação Simples.
Esta atividade foi extraída da aula Gincana Combinatória: Trabalhando os conceitos de permutação, arranjo e combinação da professora Raquel Cupolillo Simões de Sousa - Rio de Janeiro/RJ. Disponível no Portal do Professor/MEC. Acessado em 15/07/2013. Todas as informações contidas nela são de responsabilidade do autor.