Sugestão de atividade - Jogo do vai e vem: adição e subtração de números inteiros

Recursos materiais

• Papel cartão ou cartolina (tabuleiro do jogo)
• Folhas sulfites coloridas e brancas
• Régua
• Tesoura
• Pinceis coloridos
• Dados com as faces numeradas de 1 a 7
• Dados com as faces identificadas com sinais de + e –
• Tampinhas coloridas ou objetos para representarem os jogadores

Professor, o tabuleiro e as peças do jogo podem ser preparados previamente ou você pode sugerir que os alunos construam seus próprios materiais. A construção do jogo pelos alunos pode ajudá-los na elaboração, reconhecimento e compreensão do conceito de reta numérica dos números inteiros.

Comentário: Caso o professor faça opção por este caminho metodológico, recomenda-se reservar um número maior de aulas para a execução das atividades propostas.

Para a construção do jogo ou para jogar, o professor pode dividir a turma em grupos de dois, três ou quatro componentes. Defende-se que a dinâmica das atividades pode ser comprometida, caso uma equipe tenha mais de 4 integrantes por permitir que membros fiquem ociosos por um tempo longo.

CONFECÇÃO DO JOGO:

As folhas sulfites coloridas são recortadas em pequenos retângulos. Nesses cartões devem ser escritos uma sequência numérica de números inteiros positivos e outra de negativos. Recomenda-se confeccionar um retângulo maior para representar o número zero e, ainda, identifica-lo com a palavra “Largada”, pois será o ponto de início (partida) do jogo. Este retângulo será o primeiro a ser fixado no tabuleiro (papel cartão ou cartolina). Os retângulos recortados e numerados constituirão a trilha do jogo. Essa trilha será montada no tabuleiro.

Comentário: Na confecção do jogo pelos alunos, a construção do tabuleiro torna-se uma oportunidade para o professor resgatar os princípios de identificação dos números inteiros em uma reta numérica.

Ao construir o tabuleiro, não é necessário que a trilha siga em linha reta, no entanto, os números devem obedecer a uma sequência numérica. O final das trilhas, tanto dos números positivos quanto dos negativos, deve ser identificado como pontos de “Chegada” do jogo. Para isso, podem-se confeccionar retângulos usando folhas sulfites coloridas.

Quando da construção do jogo, pode ser oportuno que o professor questione os alunos quanto ao sentido dos números negativos ou, por exemplo:

• Qual é maior – 7 ou – 6?
• Para um número negativo é verdade que quanto maior o seu módulo menor é o seu valor numérico? O que significa o módulo de um número?
• Qual é o número oposto de – 5?
• O que significa perguntar ou localizar o oposto (simétrico) de um número?

Com essas perguntas, espera-se um resgate dos conceitos dos números inteiros, como por exemplo: oposto ou simétrico de um número, módulo de um número inteiro.

A figura a seguir é uma sugestão de estruturação da trilha do tabuleiro, mas outras formas podem ser construídas.

Figura 1: Sugestão de estruturação do tabuleiro.



Fonte: arquivo do autor.

É prudente lembrar que quanto maior a sequência, maior o tempo gasto com a atividade do jogo, porém maiores serão as possibilidades de diversificar as jogadas e as situações vivenciadas.

Aconselha-se, antes de iniciar o jogo, que o professor solicite aos alunos a construção de um quadro com 5 colunas e várias linhas em folhas sulfites brancas A4. É importante que se deixe espaço para que novas linhas sejam incluídas no quadro, pois essas linhas serão usadas para que os alunos registrem as jogadas de cada rodada. Outra observação a ser feita na construção do quadro é que a 5ª coluna seja maior e inicialmente deixada em branco para futura formalização das operações.

Quadro 1: Exemplo de quadro para registro das jogadas.

Número da rodada	Valor numérico da posição em que estou	Número sorteado	Valor numérico da posição em que parei


Fonte: arquivo do autor.

Antes de iniciar o jogo, todos os jogadores devem registrar na primeira linha da coluna “Número da rodada” como sendo a 1ª e na coluna “Valor numérico da posição em que estou”, o valor zero, pois todos os jogadores iniciarão da posição “Largada”, que no jogo é representada pelo valor zero, conforme explicado anteriormente (quadro 1).

Dessa forma, todos terão as seguintes informações no seu quadro para a primeira rodada:

Quadro 1: Exemplo de quadro para registro das jogadas.

Número da rodada	Valor numérico da posição em que estou	Número sorteado	Valor numérico da posição em que parei
1ª	0


Fonte: arquivo do autor.

Cada integrante da equipe escolhe uma tampinha de cor diferente para se identificar no jogo. Em seguida, o grupo deve definir a ordem de cada jogador a realizar sua jogada. Conforme orientam os Parâmetros Curriculares Nacionais (PCN), ao lidarem com situações de jogos com regras, os alunos conseguem perceber que as combinações são definidas pelos próprios jogadores e que só podem jogar em função da jogada do outro. Esse aspecto torna-se importante por permitir que os alunos conquistem um desenvolvimento cognitivo, emocional, moral e social, além de um estímulo para ampliação do seu raciocínio lógico (BRASIL, 1997).

Para a formalização posterior das operações, aconselha-se que o professor oriente os jogadores a registrarem todos os passos da jogada conforme identificado em cada coluna do quadro. Em seguida, o professor disponibiliza um dado com as faces numeradas e outro, com as faces identificadas com os sinais positivo ( + ) e negativo ( – ) para cada grupo. Os dois dados deverão ser lançados por cada jogador simultaneamente, conforme podem ser visualizados na imagem a seguir.

Figura 2: Detalhe dos dados e das tampinhas que representam os jogadores.



Fonte: imagem do autor.

Pondera-se que é necessário esclarecer aos jogadores que cada peça deve ser movida de acordo com a quantidade de “casas” sorteadas no dado numérico. Além disso, quando o valor sorteado corresponder ao sinal positivo ( + ), o jogador deve mover a sua peça para a direita, ou seja, na ordem crescente. Caso o sinal sorteado seja o negativo ( – ), a peça deve ser movida para a esquerda, ou seja, na ordem decrescente dos números.

Assim, supondo que a imagem anterior representa a primeira jogada, tem-se sorteado o sinal + e o número 7. O jogador, então, deve mover a peça que o representa 7 casas para a direita e registrar a sua jogada, que ficará registrada da seguinte forma:

Quadro 1: Exemplo de quadro para registro das jogadas.

Número da rodada	Valor numérico da posição em que estou	Número sorteado	Valor numérico da posição em que parei
1ª	0	+ 7	+ 7
2ª	+ 7

Fonte: arquivo do autor.

Porém, se na segunda rodada, este jogador sortear o sinal negativo (–) e o valor 6, este deverá mover a sua peça 6 casas numéricas para a esquerda e, novamente, deverá registrar a sua jogada que se configurará da seguinte forma:

Quadro 1: Exemplo de quadro para registro das jogadas.

Número da rodada	Valor numérico da posição em que estou	Número sorteado	Valor numérico da posição em que parei
1ª	0	+ 7	+ 7
2ª	+ 7	– 6	+ 1

Fonte: arquivo do autor.

E assim, sucessivamente, até que um dos jogadores alcance a Chegada da trilha do tabuleiro. Pode-se também dar continuidade ao jogo até que todas as posições dos jogadores do grupo se definam.

Comentário: O professor pode, também, sugerir uma “competição” entre os grupos ou entre salas na forma de campeonato. Para isso, os vencedores de cada grupo devem formar grupos para novas partidas e, assim, até restarem dois jogadores para fazerem uma partida final. Nesse caso, é aconselhável reservar um maior número de aulas, caso se opte por essa metodologia de aplicação do jogo.

Comentário: O jogo proposto pode ser utilizado para reforçar o conhecimento do aluno acerca da adição dos números inteiros, mas também pode ser o “disparador”, para se introduzir essa operação.

Com o registro das jogadas, cada jogador terá um quadro próprio correspondente às suas próprias jogadas. Aconselha-se que essas informações sejam usadas para formalização da adição com os números inteiros. No caso do jogo ser um elemento disparador, é importante que o professor escolha exemplos que possam garantir a maior diversidade possível de situações vivenciadas pelos alunos nessa fase. Por isso, aconselha-se que as situações em que os alunos tiveram que efetuar operações, mesmo que sem perceberem: (+) + (+), ( – ) +( – ) , (+) +( –),( –) +( +) sejam socializadas para que os alunos percebam o que acontece com os resultados e a partir daí, estabeleçam a regra da adição com os números inteiros, considerando os sinais iguais ou diferentes

Comentário: Durante a realização dos jogos, aconselha-se ao professor ficar atento às jogadas dos alunos. Para isso, torna-se importante que o docente circule pelo ambiente buscando garantir esse momento.

É prudente lembrar que antes de socializar os exemplos, o professor deve instigar os alunos pedindo para analisem os seus quadros e que tirem individualmente, suas conclusões. Espera-se que os discentes percebam que a soma do valor registrado na coluna “Valor numérico da posição em que estou” com o “Número sorteado” é igual ao valor da coluna “Valor numérico da posição em que parei”.

Após esse momento, sugere-se que o professor solicite aos alunos que registrem na última coluna, até então em branco, a inscrição “Formalizando”. Em seguida, devem ser registradas as operações “efetuadas” durante a realização do jogo quando do sorteio de cada valor em cada rodada por cada integrante do grupo.

Lembra-se que outra conclusão importante a ser alcançada pelos alunos são as regras de sinais das operações de adição e subtração com números inteiros. Assim, quando os sinais são diferentes, o resultado é a subtração dos valores absolutos com a conservação do sinal do valor do maior módulo. E quando os sinais são iguais, o resultado é a soma dos valores absolutos e seu sinal é conservado.

ENRIQUEÇA SUA AULA

Os quadros de valores podem ser registrados, posteriormente, usando um software de planilhas de cálculos como, por exemplo, o Excel do Office do Windows. Como o quadro simulado a seguir:

Quadro 1: Exemplo de quadro para registro das jogadas.

Número da rodada	Valor numérico da posição em que estou	Número sorteado	Valor numérico da posição em que parei
1ª	0	4	4
2ª	4	-6	-2
3ª	-2	5	3
4ª	3	-7	-4
5ª	-4	-5	-9
6ª	-9	4	-5

Fonte: arquivo do autor.

Sugere-se aos professores que, ao utilizarem os softwares de planilhas de cálculos, os alunos podem ser desafiados a elaborarem e criarem fórmulas para a coluna “Valor numérico da posição em que parei” que apresente o resultado das operações com os valores a serem lançados na coluna “Número sorteado”. Para isso, o professor deve ter certo domínio do software quanto à sua formatação e configuração.

Adverte-se, ainda, apesar de ser um apoio no processo de ensino e aprendizagem das operações com números inteiros, os alunos podem apresentar dificuldades, uma vez que, o software citado, não apresenta a opção de subtração, apenas da soma.

Comentário: Algumas configurações são necessárias para que o software aceite o trabalho com números negativos:

1. Nas três colunas: “Valor numérico da posição em que parei”, “Número sorteado” e “Valor numérico da posição em que parei”, as células em que os valores serão lançados devem ser selecionados e o operador deve dar um clique com o botão direito do mouse e escolher a opção “Formatar células”.
2. Na opção “Número”, zerar o número de casas decimais e na coluna “Categorias”, selecionar a opção “Número” e, ainda, na caixa “Números negativos”, deve-se escolher uma das opções com sinal de negativo.
3. Após registrar os números na coluna “Valor numérico da posição em que parei” deve-se digitar a fórmula de cálculo da adição entre esses valores. Para isso, é preciso digitar o sinal de igual (=) e depois a soma entre a referência da célula da coluna “Valor numérico da posição em que estou” e a referência da célula da coluna “Número sorteado”. Por exemplo, se os valores a serem adicionados forem lançados nas células B3 e C3, respectivamente, a fórmula será: =B3+C3, conforme destacado na ilustração a seguir, onde está representada a digitação da fórmula referente à célula D3 (Figura 3).

Figura 3: Exemplo de fórmula a ser digitada pelo aluno.



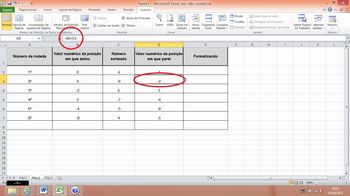
Fonte: imagem do autor.

Outra configuração possível, na coluna “Valor numérico da posição em que estou”, é defini-la para apresentar o valor da célula da linha superior, na coluna identificada como: “Valor numérico da posição em que parei”. Para isso, na célula em que se deseja que o valor apareça, deve-se colocar o sinal de igual e a referência da linha e coluna do valor desejado, por exemplo, para a segunda rodada, digitar na segunda célula numérica da segunda coluna, conforme destacado na ilustração a seguir (Figura 4).

Figura 4: Exemplo de definição valor coluna “Valor numérico da posição em que estou”.



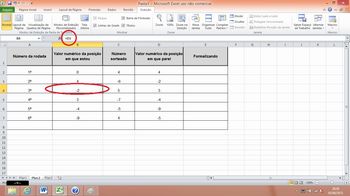
Fonte: imagem do autor.

---

Esta atividade foi extraída da aula Jogo do vai e vem: adição e subtração de números inteiros do professor Éderson de Oliveira Passos - Uberlândia/MG. Disponível no Portal do Professor/MEC. Acessado em 15/07/2013. Todas as informações contidas nela são de responsabilidade do autor.