Sugestão de atividade - Relacionando a área do triângulo e abscissa
Utilize a atividade abaixo para perceber com a turma como a variação da abscissa influencia a área de um triângulo dado, observando seu comportamento através da interação com a cena dada.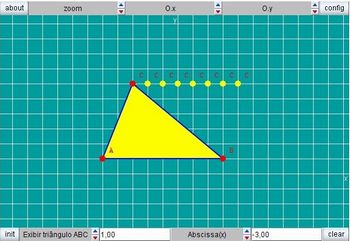
Figura 1: Abscissa x Área do triângulo - Imagem da autora
Para realizar esta atividade acesse:http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/FConstanteGeom1.html
Observe a figura. Nela, os pontos A e B são fixos e C pode ter o valor da abscissa alterado.
a) Escolha três valores para a abscissa x alterando na caixa correspondente e exiba o triângulo formado em cada caso. Comentário: É importante que os alunos visualizem as diferentes possibilidades antes de tentar obter a solução. Cada aluno escolherá os valores de entrada.
b) Calcule a área de cada um deles.
Comentário: Os alunos devem perceber que a área é a mesma.
c) Dê o conjunto de valores que x pode assumir.
Comentário: Ressalte que esta resposta é dada em função da análise feita na parte gráfica da atividade. Pergunte a turma se existem outras possibilidades de atribuição de valores de abscissa para construir os triângulos. Daí surge a resposta dada. É muito importante que os alunos a utilizem para fazer as experimentações, pois, através dela, é possível trabalhar com um maior número de exemplos o que amplia as oportunidades de aprendizagem durante a aula ao reduzir o nível de abstração via representações gráficas.
d) Compare as alturas e as bases desses triângulos.
e) A área dos triângulos depende dos valores de x? Justifique.
f) Determine o(s) valor(es) de x para que o triângulo ABC seja:
i) Um triângulo isósceles de base AB.
ii) Um triângulo retângulo
g) O tipo de triângulo depende dos valores de x?
h) Qual(is) é(são) o(s) valor(es) que a ordenada (y) pode assumir? Justifique.

a) Por exemplo, x=2, x=5 e x=6.
b) A área que deve ser encontrada é 40 u.a..
c) Nesta atividade a abscissa pode assumir qualquer número inteiro, porém podemos estender este conceito para qualquer número real.
d) Ambas são fixas.
e) Não, pois a alteração no valor da abscissa não muda o valor da área.
f) i) Um triângulo isósceles de base AB. A abscissa deve ser igual a -1;
ii) Um triângulo retângulo. A abscissa pode ser igual a -5 ou 3.
g) Sim, tanto sua classificação quanto a medida dos lados quanto em relação a medida dos ângulos.
h) Neste caso não ocorre variação no valor da ordenada pois a altura do triângulo não é alterada O valor da ordenada é 6.
Após concluir esta atividade a turma deve perceber que embora a abscissa sofra alterações, o valor da área correspondente a cada triângulo formado fica inalterado, uma vez que a base e a altura permanecem constantes.
Esta atividade foi extraída da aula A Geometria na Construção do Conceito de Funções Constantes e Lineares da professora Raquel Cupolillo Simões de Sousa - Rio de Janeiro/RJ. Disponível no Portal do Professor/MEC. Acessado em 15/07/2013. Todas as informações contidas nela são de responsabilidade do autor.

