Disciplina - Matemática

Sugestão de atividade - Quantos tijolos precisarei para concluir a minha obra?

Durante a construção de uma casa, constantemente os profissionais envolvidos precisam fazer cálculos de áreas para orçar materiais. Um exemplo simples é o cálculo da alvenaria. Quantos tijolos precisarei para concluir a minha obra? Sugiro uma atividade em grupos. Os alunos deverão responder a pergunta acima considerando o desenho abaixo: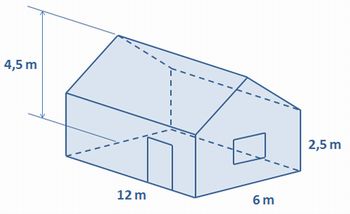


Imagem do autor


Dados:
  • Dimensões da porta: 2,20 x 0,80 m;
  • Dimensões da janela: 2,00 x 1,50 m;
  • Dimensões dos tijolos:


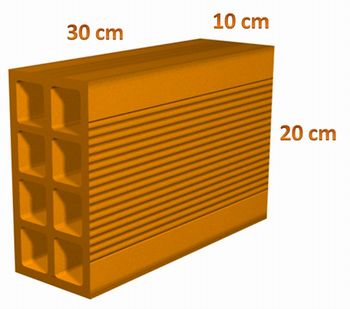
Imagem do autor

  • Acrescentar 10% do total calculado;
  • Arredondar sempre para “cima”.

Monitore cada grupo e interaja nas estratégias adotadas pelos alunos. Os grupos devem encontrar algo em torno de 1013 tijolos. Explique ainda o porquê das diferenças nos resultados encontrados.

Outra atividade, bastante interessante, mostra a aplicação da matemática no cotidiano do pedreiro. Quando um pedreiro precisa construir uma parede, perpendicular a outra parede, ele usa o seguinte método:          
  • Ele marca (com dois pregos) uma distância de 60 cm na parede já construída;          
  • Com duas linhas, uma de 80 cm e outra de 1m (cada uma presa num prego), ele determina o ponto de encontro entre as extremidades;
  • Por fim ele traça uma linha entre o este ponto de encontro com o primeiro prego.

Veja na figura:


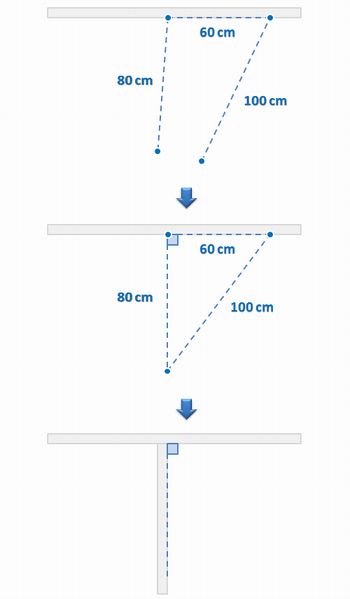
Imagem do autor


Antes de expor este método, lance o desafio para os grupos:

  • Como poderíamos construir uma nova parede perpendicular a uma parede já construída?

Discuta as estratégias manifestadas.

Após a demonstração do método acima, faça os seguintes questionamentos aos grupos:

  • Como podemos garantir, com este método, que a nova parede será perpendicular a outra?
  • Que outros valores inteiros o pedreiro poderia usar?  
  • Por que o pedreiro não usa valores menores, 30, 40 e 50 cm, por exemplo?

A colocação de pisos gera outros problemas matemáticos. Proponha o seguinte problema.

Considere o desenho abaixo e calcule:


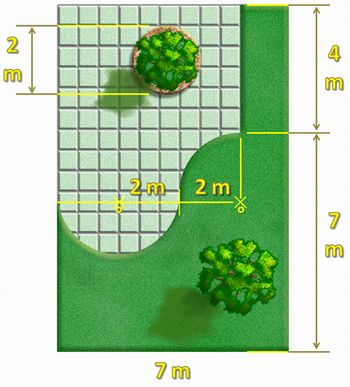
Imagem do autor

  1. A área do piso de cerâmica (acrescentar 10% do total);
  2. A área de grama (acrescentar 10% do total);
  3. O custo de materiais (grama e cerâmica), considerando R$ 5,00 o m2 da grama e R$ 15,00 o m2 da cerâmica.
Os alunos devem encontrar como respostas:
  1. 39,6 m2;
  2. 41,65 m2;
  3. R$ 802,25
Discuta com os alunos o motivo de se acrescentar 10% nos cálculos. Para finalizar vamos abordar um problema na construção de escadas. Consideremos A como o afastamento horizontal e H como a altura. Para um degrau teremos:


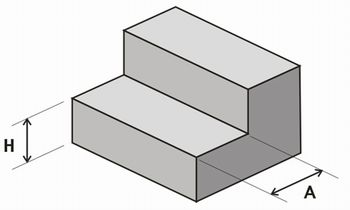
Imagem do autor


Vamos, primeiramente, a um problema simples (ainda em grupos). Um carpinteiro construirá uma escada de madeira. Considere uma altura a vencer de 3 m, e degraus de 15 cm de altura e 28 cm de afastamento.
  1. Quantos degraus serão necessários?
  2. Qual será o afastamento horizontal total?
  3. Qual será o ângulo de inclinação (em relação ao solo) da escada?

Os alunos deverão encontrar o seguinte resultado:


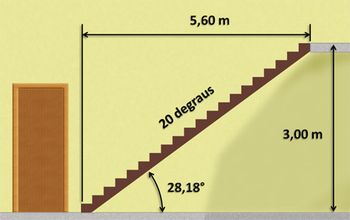
Imagem do autor


Agora vamos aumentar a complexidade, e usar a ferramenta Solver do Microsoft Excel. No laboratório de informática, peça para os alunos criarem a planilha abaixo:


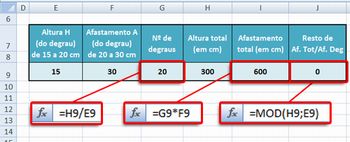
Imagem do autor


Com a planilha pronta vamos analisar o problema: Com uma escada, queremos “vencer” 3 m de altura. Vamos imaginar que o engenheiro exigiu que a altura dos degraus ficasse entre 15 e 20 cm e o afastamento de cada degrau entre 20 e 30 cm. Por conta de uma porta, o afastamento total não deve ultrapassar 4,32 m. Quais seriam as alturas e afastamentos ideais dentro dessas condições? Poderia existir mais de uma opção? Quantos degraus a escada teria? Deixe que os alunos modifiquem a planilha em busca de valores ideais. Depois, com ajuda da macro Solver, vamos resolver o problema. Veja:


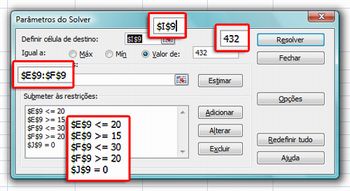
Imagem do autor


A célula destino é a I9, que deve atingir o valor 432 cm, variando as células E9 e F9, com as restrições listadas. A última restrição é J9 = 0. J9 armazena o resto da divisão da altura total a ser vencida pela altura do degrau. O resultado desta divisão nos dará o número de degraus. Como queremos um número inteiro, o resto desta divisão deverá ser zero. Explore esta estratégia com os alunos.

Veja que a macro Solver pode encontrar mais de uma solução:


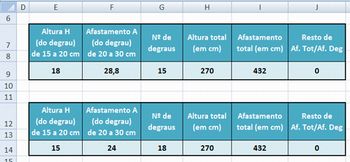
Imagem do autor


Discuta com os alunos as vantagens e desvantagens de cada solução. Ainda podemos usar a macro Solver para determinar as dimensões dos degraus tendo um afastamento total mínimo. Para isso basta marcar a opção Min na macro Solver.

Veja:


Imagem do autor


Repare que com uma altura de 15 cm, e um afastamento de 20 cm em cada degrau, conseguimos um afastamento total de apenas 3,60 m.

Outra discussão que o professor pode propor é quanto à estrutura de andaimes construídos por pedreiros. Discuta com os alunos qual dos andaimes abaixo apresenta maior estabilidade.


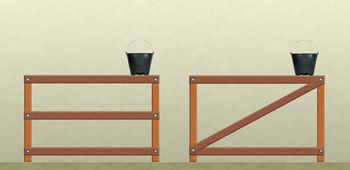
Imagem do autor


Relacione as formas usadas nesses andaimes com as propriedades de rigidez que o triângulo apresenta. Esta propriedade pode ser testada com réguas articuladas. Veja:


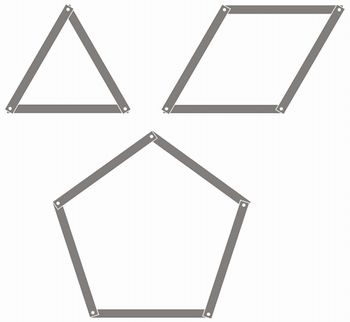
Imagem do autor


Mostre a importância dessa propriedade dos triângulos nas estruturas das construções:


Disponível em: (http://www.lem.ep.usp.br/pef2309/antigo/2002.1/2002pontes/Pontes%20-%20Estradas%20de%20Ferro.htm)
Esta atividade foi extraída da aula Onde Está a Matemática na Engenharia Civil? do professor Guilherme Erwin Hartung - Petrópolis/RJ. Disponível no Portal do Professor/MEC. Acessado em 15/07/2013. Todas as informações contidas nela são de responsabilidade do autor.
Recomendar esta página via e-mail: