Sugestão de atividade - Mosaico
Proponho que os alunos formem grupos e recebam o seguinte questionamento. Com que formas regulares iguais podemos construir um mosaico sem que haja espaços entre as formas? Os alunos concluirão que as formas possíveis são os triângulos equiláteros, quadrados ou hexágonos. Discuta com seus alunos o porquê das outras formas não servirem. Relacione essas conclusões com o fato dos ângulos internos dessas figuras serem divisores de 360.
Vamos considerar agora, prismas com bases isoperimétricas. Cada grupo deve receber três tiras de cartolina com dimensões 12 x 1 cm cada. Pensando em prismas com essas bases, peça para os grupos construírem os três prismas com dobraduras. Veja na figura abaixo:
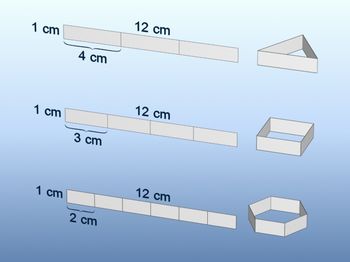
Peça agora para que eles calculem o volume de cada prima. Os alunos perceberão que os volumes dos prismas serão aproximadamente 6,92 cm3, 9 cm3 e 10,38 cm3 respectivamente e que, apesar das áreas laterais serem iguais, o prisma hexagonal oferece o maior volume. Neste momento discuta com os grupos qual a relação desta atividade com a construção dos alvéolos, pelas abelhas, para armazenar o mel produzido pelas mesmas. Mas a economia das abelhas vai além. Em rigor, os alvéolos não são prismas. A base do alvéolo não é plana e é constituída de três losangos. Esta pequena diferença faz com que as abelhas ganhem um alvéolo a cada 50. Exiba o vídeo abaixo.
(http://www.youtube.com/watch?v=5mKJk8-l1lY)
Conclua a atividade enfatizando a relação entre a matemática e a natureza.
Esta atividade foi extraída da aula Volume x Área Superficial uma Questão de Economia do professor Guilherme Erwin Hartung - Petrópolis/RJ. Disponível no Portal do Professor/MEC. Acessado em 15/07/2013. Todas as informações contidas nela são de responsabilidade do autor.

