Sugestão de atividade - Os balonistas e o arremesso da fita
O objetivo da atividade é introduzir o cálculo da probabilidade condicional de dois eventos.
Fonte: http://t0.gstatic.com/images?q=tbn:ANd9GcT01y56pCK-Cm_p9BtS0t-Pdj6sGv4aF2Ktf66abCMfve4iS57crA
Enfatize que, apesar de não parecer, o balonismo também é um esporte radical e que dentro das suas modalidades de competição existe o Fly In, onde os pilotos devem jogar uma fita em um alvo estrategicamente escolhido, depois de decolar a uma distância de, no mínimo, 3 km.

1. Solicite que os alunos realizem as etapas a seguir:
1.1. Construa um alvo com dois polígonos de tamanhos diferentes, de forma que haja uma interseção entre os mesmos. Chame a região menor de A e a maior de B.
1.2. Considerando a a malha quadriculada como espaço amostral, qual é a probabilidade de a fita cair em A?
1.3. Considere agora que, ao arremessar a fita "o praticante percebeu que a mesma caiu na região maior (B)". Analisando a malha quadriculada, defina se o espaço amostral se altera e determine-o caso ocorra tal alteração.
Nota: A turma deve perceber analisando a malha quadriculada, que o espaço amostral diminuiu, ficando restrito à região B.
1.4. Sabendo que a fita caiu em B, considere a possibilidade desta fita cair exatamente em A. Chame este evento de C. O que significa este evento?
1.5. Qual é a probabilidade do evento C?
Nota: A turma deve perceber que a probabilidade do evento "a fita cair na região A" foi alterada pela presença do evento "o praticante percebeu que a fita caiu na região B".
2. Permita aos alunos um momento para análise e desenvolvimento da situação proposta.
3. Estabeleça a troca de ideias com a turma para verificar o desenvolvimento de cada item utilizando o quadro de giz.

1. Um exemplo:
1.1
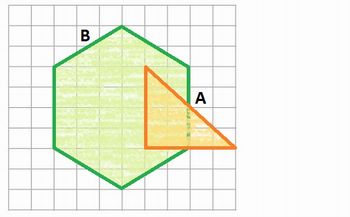
Imagem da autora
1.2. A probabilidade de a fita cair na região A é de 8%.
1.3. O espaço amostral se altera passando a ser apenas a região B.
1.4. O evento C significa que a fita deve cair ao mesmo tempo em B e em A e que é a interseção das duas regiões.
1.5. A probabilidade do evento C, interseção dos eventos A e B, é aproximadamente 0,17%.
Informe à turma que este último resultado representa a probabilidade de a fita cair na região A, condicionada ao fato de ela ter caído em B.
Esta atividade foi extraída da aula Esportes Radicais, Probabilidades e Geometria: Um diálogo possível da professora Raquel Cupolillo Simões de Sousa - Rio de Janeiro/RJ. Disponível no Portal do Professor/MEC. Acessado em 15/07/2013. Todas as informações contidas nela são de responsabilidade do autor.

