Galerias de Imagens > > Geometrias
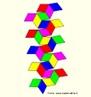
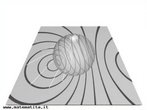
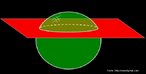
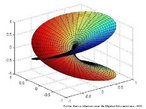
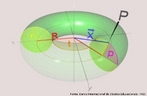
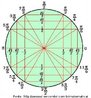
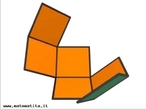
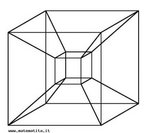
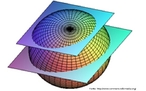
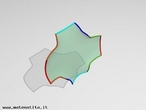
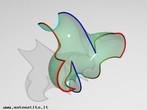
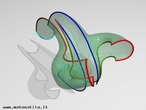
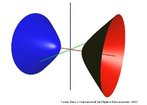
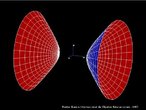
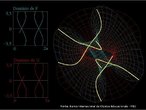
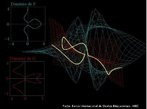
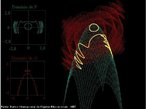
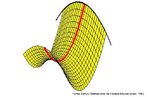
Fita de Moebius
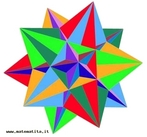
Fonte: http://www.matematita.it
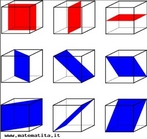
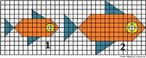
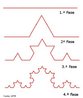
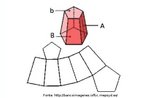
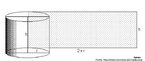
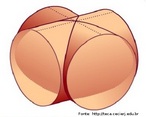
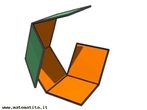
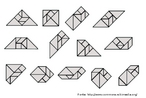
Em 1858, o matemático alemão Auguste Ferdinand Möbius pesquisando o desenvolvimento de uma Teoria dos Poliedros, em continuidade aos estudos de Euler, descobriu uma curiosa superfície. A fita que levou seu nome é um objeto bidimensional que tem superfície única. Ela pode ser construída em três dimensões da seguinte maneira: pegue uma tira de papel retangular, vire uma das pontas curtas 180 graus em relação à outra ponta curta, e una as duas pontas. Agora é possível começar de um ponto A na superfície da fita, e traçar um caminho ao longo da fita, passando por um ponto que aparentemente está no outro lado do ponto de partida. Em termos matemáticos ela é definida como uma superfície não orientável, o que significa dizer que uma linha perpendicular ao plano não tem a mesma direção em todos os pontos da superfície. O que faz da fita algo interessante são algumas de suas caracteŕisticas como, por exemplo: 1. Se ela for cortada ao meio, ao longo de seu comprimento, em vez de termos duas tiras separadas, teremos uma tira mais longa contendo duas meia-voltas. 2. Novamente cortando como antes, teremos agora duas tiras interligadas de forma curiosa. 3. Se cortarmos ao longo do comprimento, a uma distância de 1/3 da largura a partir de uma das margens e veja o que acontece! Se tomarmos a tira de papel e, ao invés de dar meia-volta, dermos uma, duas ou mais voltas e colarmos as extremidades, teremos figuras surpreendentes denominadas Anéis Paradrômicos.



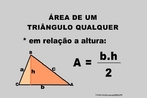
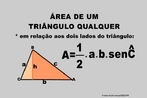

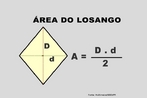
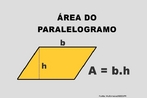
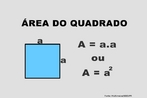
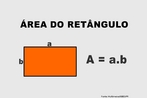
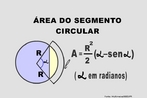
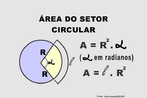






























































































































































































































![Com a imagem das pirâmides de Gizé - Keóps, Quéfrem e Miquerinos - Egito, o Professor pode mostrar a relação entre elementos da Matemática e do cotidiano. As três pirâmides em Gizé são os maiores monumentos do mundo erguidos por homens. Elas foram construídas como tumbas reais para os Reis Kufu (Keóps), Quéfren, e Miquerinos (pai, filho e neto). A maior delas, que mede 147 m de altura (equivale a um prédio de 49 andares), chamada Grande Pirâmide, foi construída cerca de 2550 A.C. para o Rei Kufu, no auge do antigo reinado do Egito. [...] A Grande Pirâmide, de mais de 450 pés de altura, é a maior de todas as 80 pirâmides do Egito. Se a Grande Pirâmide fossena cidade de Nova York, ela poderia cobrir sete quarteirões da cidade. Todos os quatro lados são quase que exatamente do mesmo comprimento, centímetro por centímetro. Isso mostra como os antigos egípcios estavam avançados na matemática e na engenharia, numa época em que muitos povos do mundo ainda eram caçadores e andarilhos. A Grande Pirâmide manteve-se como a mais alta estrutura feita pelo homem até a construção da Torre Eiffel, em 1889, cerca de 4.500 anos depois da construção da pirâmide.](http://www.matematica.seed.pr.gov.br/modules/galeria/uploads/3/thumb_622piramidesgize.jpg)