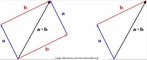
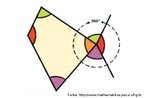
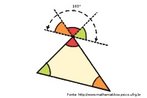
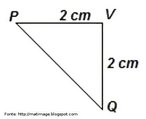
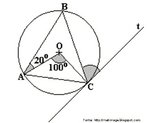
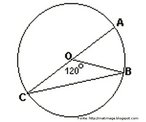
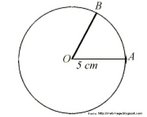
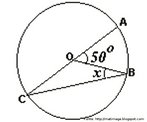
Galerias de Imagens > > Geometrias
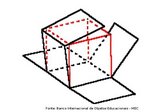
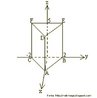
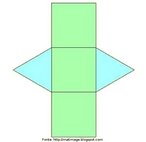
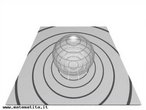
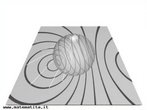
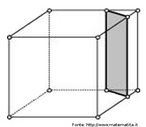
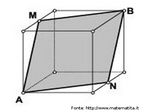
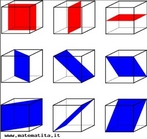
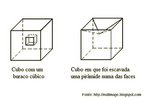
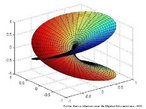
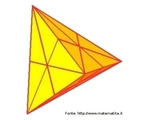
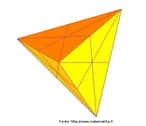
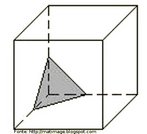
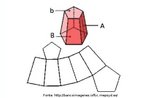
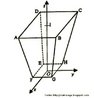
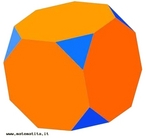
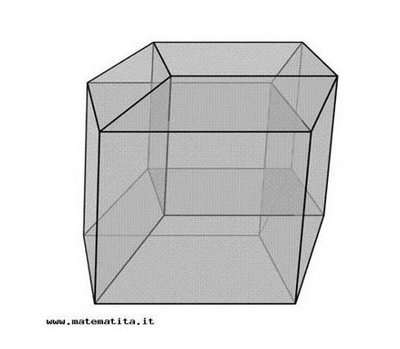
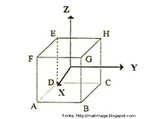
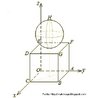
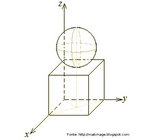
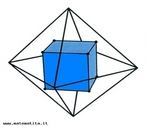
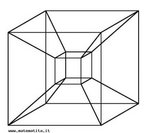
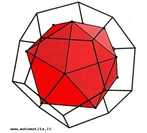
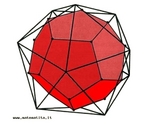
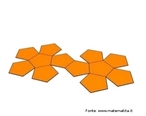
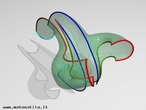
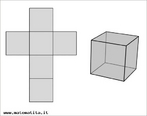
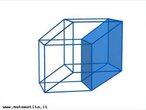
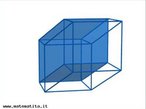
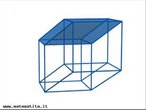
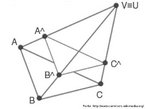
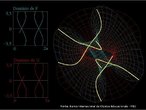
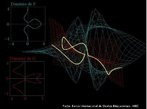
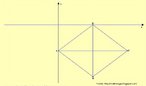
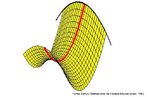
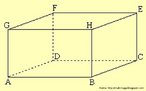
Hipercubo
Fonte: http://www.matematita.it
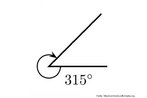
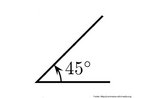
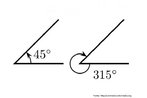
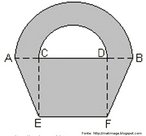
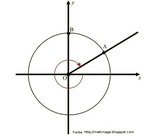
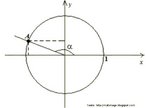
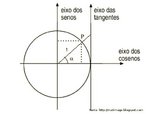
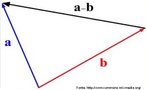
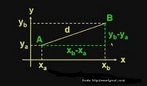
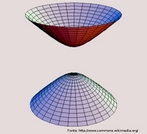
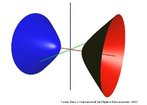
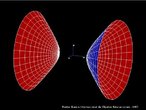
O hipercubo é um objeto matemático que representa, geometricamente, um cubo na quarta dimensão. A diferença entre um espaço de dimensão quatro e um espaço de dimensão um, dois ou três é que nessas podemos fazer representações geométricas identificando os objetos matemáticos representados, enquanto que naquela não temos como representar os objetos matemáticos pertencentes a ela. Contudo, é possível representar um objeto de dimensão alta em um espaço de dimensão mais baixa. Isso pode nos dar uma idéia da aparência desse objeto. Para tanto utiliza-se de certos artifícios como, por exemplo, a perspectiva, ou seja, para entendermos a quarta dimensão é necessário termos claros alguns conceitos da geometria. É nesse sentido que esta imagem pode servir de problematização para o trabalho de conceitos como o ponto. ponto. Um ponto é a representação geométrica de posição no espaço, apesar de ser adimensional, podemos deslocá-lo em uma determinada direção e sentido o que vai constituir um segmento de reta. Temos aí a primeira dimensão e podemos trabalhar o conceito de comprimento. Da mesma forma que o ponto, podemos deslocar o segmento de reta de tal forma a obtermos um quadrado. Nossa segunda dimensão aí está e podemos trabalhar o conceito de área. Se, novamente, deslocarmos o quadrado, podemos obter um cubo, constituindo nossa terceira dimensão onde se pode trabalhar o conceito de volume. Nessa mesma lógica podemos deslocar nosso cubo perpendicularmente a todas as trajetórias anteriores. Assim obteríamos o hipercubo. Contudo, esta direção não existe em nosso espaço tridimensional. Contudo, o Professor pode estimular os estudantes a utilizarem da analogia para a construção do hipercubo. Da mesma forma que para construirmos um quadrado, unimos dois segmentos de reta paralelos pelas suas extremidades e para representarmos um cubo unimos os vértices de dois quadrados paralelos, para representarmos o hipercubo podemos unir todos os vértices de dois cubos.


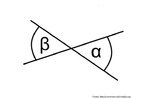
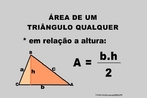
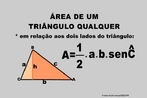

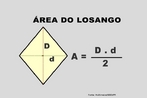
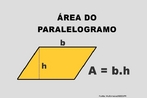
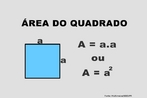
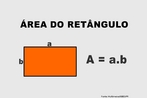
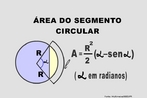
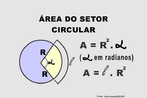
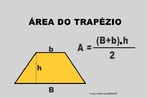





































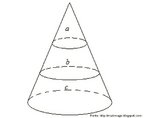
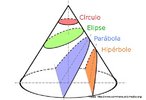



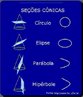
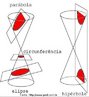



























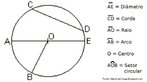



























































































































































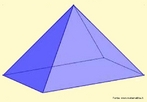
![Com a imagem das pirâmides de Gizé - Keóps, Quéfrem e Miquerinos - Egito, o Professor pode mostrar a relação entre elementos da Matemática e do cotidiano. As três pirâmides em Gizé são os maiores monumentos do mundo erguidos por homens. Elas foram construídas como tumbas reais para os Reis Kufu (Keóps), Quéfren, e Miquerinos (pai, filho e neto). A maior delas, que mede 147 m de altura (equivale a um prédio de 49 andares), chamada Grande Pirâmide, foi construída cerca de 2550 A.C. para o Rei Kufu, no auge do antigo reinado do Egito. [...] A Grande Pirâmide, de mais de 450 pés de altura, é a maior de todas as 80 pirâmides do Egito. Se a Grande Pirâmide fossena cidade de Nova York, ela poderia cobrir sete quarteirões da cidade. Todos os quatro lados são quase que exatamente do mesmo comprimento, centímetro por centímetro. Isso mostra como os antigos egípcios estavam avançados na matemática e na engenharia, numa época em que muitos povos do mundo ainda eram caçadores e andarilhos. A Grande Pirâmide manteve-se como a mais alta estrutura feita pelo homem até a construção da Torre Eiffel, em 1889, cerca de 4.500 anos depois da construção da pirâmide.](http://www.matematica.seed.pr.gov.br/modules/galeria/uploads/3/thumb_622piramidesgize.jpg)