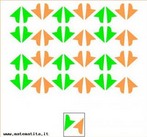
Galerias de Imagens > > Padrões e Mosaicos
Simetria
Fonte: http://matimage.blogspot.com
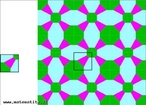
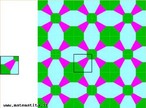
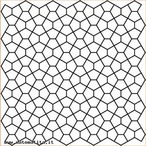
Termo originário do grego que significa "justa proporção", mas que, comumente, é definida como "harmonia resultante de certas combinações e proporções regulares" (Dicionário Aurélio), a simetria é uma propriedade facilmente encontrada na Biologia, Arquitetura, Arte, Geometria e até na Poesia. Contudo, é cada vez maior o número de pessoas que entendem a simetria como resultado de movimento e, como movimento, pode ser vivida e percebida pelo sujeito como dinâmica, como regularidade. Como movimento ela ainda pode ser percebida, compreendida e interpretada por meio dos elementos que a constituem de forma individual ou em conjunto. São eles: * Reflexão: Simetrias de reflexão ou em relação a retas são aquelas onde pontos, objetos ou partes de objetos são a imagem espelhada um do outro em relação à reta dada, chamada eixo de simetria. Repare que qualquer reta que passe pelo centro de simetria divide o objeto em duas imagens espelhadas e que o centro de simetria é o ponto médio dos segmentos unem os pontos correspondentes. * Rotação: Simetrias centrais ou rotacionais são aquelas em que um ponto, objeto ou parte de um objeto pode ser girado em relação a um ponto fixo, central, chamado centro da simetria, de tal maneira que essas partes ou objetos coincidam um com o outro um determinado número de vezes. * Translação: Transladar um objeto significa movê-lo sem girá-lo ou refletir. Cada translação tem um sentido e uma distância. * Eixo de Simetria: Em termos mais simples, o eixo de simetria é uma linha que divide uma figura em duas partes simétricas. Isto é: como se fosse a base de um espelho sobre uma figura. Ao refletir a imagem para lá do espelho cria uma imagem invertida da mesma. Com esta imagem o Professor pode trabalhar a percepção, a compreensão e a expressão das principais propriedades da simetria.